This content is from the fall 2016 version of this course. Please go here for the most recent version.
Homework 05: Analyzing the gapminder dataset using Python
Overview
Due before class Wednesday November 2nd.
The basic goal of the assignment is to implement various computational methods (e.g. data frames, lists, filtering, conditional expressions, iteration, functions) in Python. Rather than using raw programming assignments, you will demonstrate these skills in the context of analyzing the gapminder dataset, something you have already explored in R.
Fork the hw05 repository
Go here to fork the repo for homework 05.
Workflow
You are provided with a Jupyter Notebook similar to the one seen here. Fill in the chunks with the appropriate code needed to perform the requested analysis. I have already identified the questions and tasks you need to perform.
Submit the assignment
Your assignment should be submitted as a single Jupyter Notebook. Follow instructions on homework workflow. As part of the pull request, you’re encouraged to reflect on what was hard/easy, problems you solved, helpful tutorials you read, etc.
Rubric
Check minus: Notebook cannot be run. Didn’t answer all of the questions. Code is incomprehensible or difficult to follow.
Check: Solid effort. Hits all the elements. No clear mistakes. Easy to follow (both the code and the output). Nothing spectacular, either bad or good.
Check plus: Innovative use of coding elements to solve the problems (e.g. functions, conditional expressions, iterations). Adds labels to graphs. Uses techniques beyond those from the example notebooks. Successfully attempts the advanced challenge.
Import packages and setup the notebook
# Import libraries
import pandas as pd
import numpy as np
# Turn off notebook package warnings
import warnings
warnings.filterwarnings('ignore')
# print graphs in the document
%matplotlib inlineLoad the data with Pandas
Print the first five rows of the gapminder DataFrame
What is the average (mean) life expectancy for the entire dataset?
59.474439366197174What is the average (mean) life expectancy, for each continent?
continent
Africa 48.865330
Americas 64.658737
Asia 60.064903
Europe 71.903686
Oceania 74.326208
Name: lifeExp, dtype: float64For each country in Oceania, print the subset of the data for that country
Australia
country continent year lifeExp pop gdpPercap
60 Australia Oceania 1952 69.120 8691212 10039.59564
61 Australia Oceania 1957 70.330 9712569 10949.64959
62 Australia Oceania 1962 70.930 10794968 12217.22686
63 Australia Oceania 1967 71.100 11872264 14526.12465
64 Australia Oceania 1972 71.930 13177000 16788.62948
65 Australia Oceania 1977 73.490 14074100 18334.19751
66 Australia Oceania 1982 74.740 15184200 19477.00928
67 Australia Oceania 1987 76.320 16257249 21888.88903
68 Australia Oceania 1992 77.560 17481977 23424.76683
69 Australia Oceania 1997 78.830 18565243 26997.93657
70 Australia Oceania 2002 80.370 19546792 30687.75473
71 Australia Oceania 2007 81.235 20434176 34435.36744
New Zealand
country continent year lifeExp pop gdpPercap
1092 New Zealand Oceania 1952 69.390 1994794 10556.57566
1093 New Zealand Oceania 1957 70.260 2229407 12247.39532
1094 New Zealand Oceania 1962 71.240 2488550 13175.67800
1095 New Zealand Oceania 1967 71.520 2728150 14463.91893
1096 New Zealand Oceania 1972 71.890 2929100 16046.03728
1097 New Zealand Oceania 1977 72.220 3164900 16233.71770
1098 New Zealand Oceania 1982 73.840 3210650 17632.41040
1099 New Zealand Oceania 1987 74.320 3317166 19007.19129
1100 New Zealand Oceania 1992 76.330 3437674 18363.32494
1101 New Zealand Oceania 1997 77.550 3676187 21050.41377
1102 New Zealand Oceania 2002 79.110 3908037 23189.80135
1103 New Zealand Oceania 2007 80.204 4115771 25185.00911Sort gapminder by population. Make sure the sorted object replaces the existing gapminder DataFrame
Using seaborn, generate a scatterplot depicting the relationship between population and life expectancy and include a linear best fit line
import seaborn as sns<matplotlib.axes._subplots.AxesSubplot at 0x10833b2b0>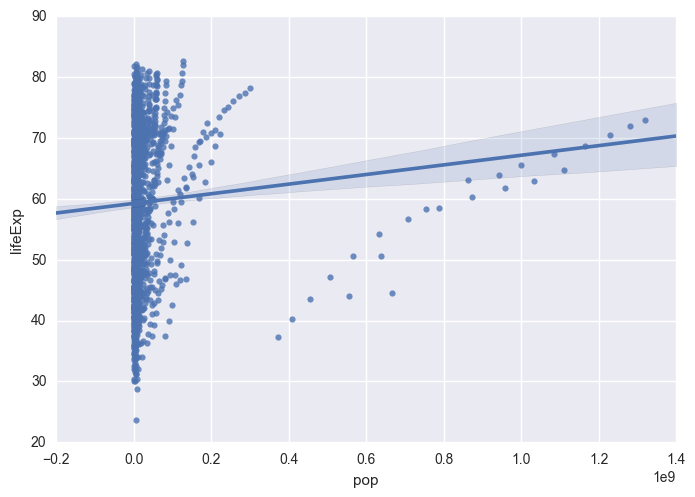
png
Generate the same graph as above, but this time log-transform the population variable
<matplotlib.axes._subplots.AxesSubplot at 0x108450518>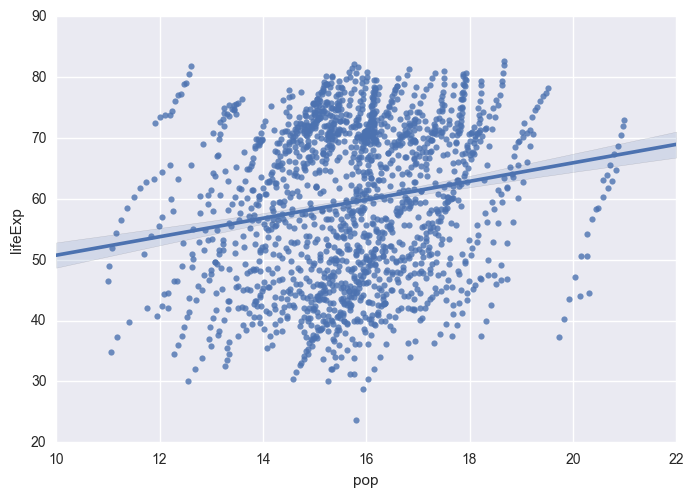
png
Write a Function
(To Assess the Relationship Between Year and Life Expectancy for a Given Country)
Here the goal is to write a basic function, “life_expectancy”, that incorporates your work above.
By default, the function should return a scatterplot of life-expectancy versus years for a given country. [Hint: Subset the data for a specific country, similar to a problem above]
Once you subset the data, the function should do one of two things: * (1) return a graph [or] * (2) return a graph and model results.
Thus, your function should have arguments and output as follows:
* Arguments:
Country (required): The name of a specific country, such as "Australia"
Model (optional): Build and Return a Model Results, #Hint, set the default to be False
* Output:
(1) - Default: A scatterplot of the relationship with best fit line
(2) - Model: The above graph AND the model resultsOf course, we have not yet covered modeling in Python.
To run a linear model, we can use the library statsmodels, to predict life expectancy by year.
Example for this problem:
import statsmodels.formula.api as sm #Import Package
model = sm.ols(formula = 'lifeExp ~ year', data = gapminder).fit() #Fit OLS Model
results = model.summary() #Get Results
print(results) # Print
#Hint: Use this Code in Your Function.
#You will need to replace data = gapminder, with the data subset for a specific country. OLS Regression Results
==============================================================================
Dep. Variable: lifeExp R-squared: 0.190
Model: OLS Adj. R-squared: 0.189
Method: Least Squares F-statistic: 398.6
Date: Tue, 25 Oct 2016 Prob (F-statistic): 7.55e-80
Time: 16:40:53 Log-Likelihood: -6597.9
No. Observations: 1704 AIC: 1.320e+04
Df Residuals: 1702 BIC: 1.321e+04
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [95.0% Conf. Int.]
------------------------------------------------------------------------------
Intercept -585.6522 32.314 -18.124 0.000 -649.031 -522.273
year 0.3259 0.016 19.965 0.000 0.294 0.358
==============================================================================
Omnibus: 386.124 Durbin-Watson: 1.962
Prob(Omnibus): 0.000 Jarque-Bera (JB): 90.750
Skew: -0.268 Prob(JB): 1.97e-20
Kurtosis: 2.004 Cond. No. 2.27e+05
==============================================================================
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 2.27e+05. This might indicate that there are
strong multicollinearity or other numerical problems.# write your function hereExample Results for the Function
Your function should be able to produce these results:
# Result for a Country (No Model)
life_expectancy("Afghanistan")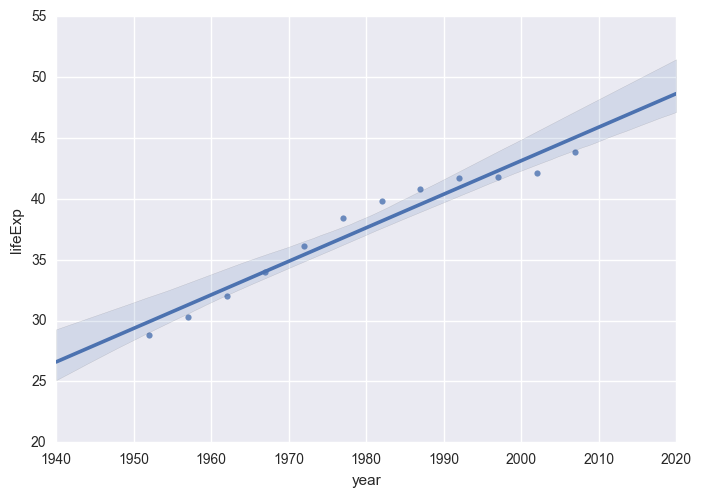
png
# Result for a Country (Model = True)
life_expectancy("New Zealand", True) OLS Regression Results
==============================================================================
Dep. Variable: lifeExp R-squared: 0.954
Model: OLS Adj. R-squared: 0.949
Method: Least Squares F-statistic: 205.4
Date: Tue, 25 Oct 2016 Prob (F-statistic): 5.41e-08
Time: 16:49:02 Log-Likelihood: -13.321
No. Observations: 12 AIC: 30.64
Df Residuals: 10 BIC: 31.61
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [95.0% Conf. Int.]
------------------------------------------------------------------------------
Intercept -307.6996 26.630 -11.554 0.000 -367.036 -248.363
year 0.1928 0.013 14.333 0.000 0.163 0.223
==============================================================================
Omnibus: 1.899 Durbin-Watson: 0.530
Prob(Omnibus): 0.387 Jarque-Bera (JB): 1.086
Skew: -0.420 Prob(JB): 0.581
Kurtosis: 1.789 Cond. No. 2.27e+05
==============================================================================
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 2.27e+05. This might indicate that there are
strong multicollinearity or other numerical problems.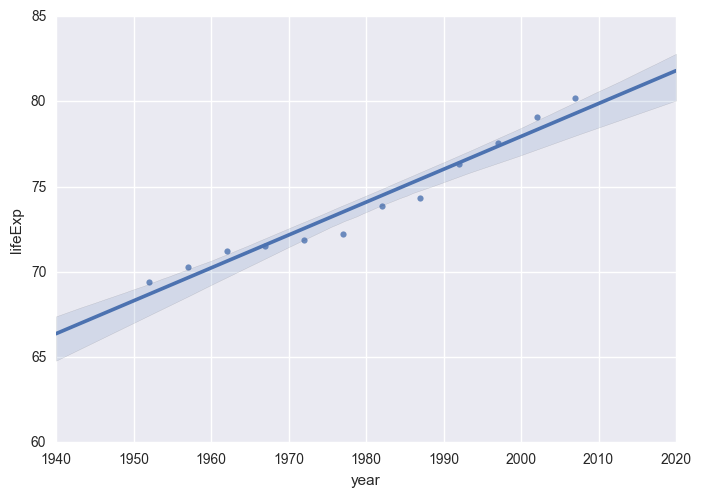
png
Advanced Challenge (Optional)
Assess the relationship between year and life expectancy
As you know already, the general trend is that over time life expectancy increases, but the trend is different for each country. Some experience a greater increase than others, whereas some countries experience declines in life expectancy. You can use whatever method you wish to assess and explain this relationship using Python.
- You could draw a graph
- You could draw a graph which visualizes the differing relationships between countries
- You could estimate a correlation coefficient
- You could estimate a statistical model - note that the notebook as written uses Python 2. For the most part it works with Python 3 though.
- You could estimate a statistical model for each country
Use whichever method you think you can master before the assignment is due. Some of you may just stick to basic graphs and tables, while others might build a statistical model using statsmodel. Obviously the more advanced technique you use, the higher your ceiling will be for your evaluation. But don’t spend 10 hours getting this to work! Go with what you can accomplish in a reasonable amount of time.
This work is licensed under the CC BY-NC 4.0 Creative Commons License.