This content is from the fall 2016 version of this course. Please go here for the most recent version.
Statistical learning: resampling and decision trees
library(tidyverse)
theme_set(theme_bw())Objectives
- Define resampling methods
- Review the validation set approach using linear regression
- Explain leave-one-out cross-validation
- Explain \(k\)-fold cross-validation
- Demonstrate how to conduct cross-validation on generalized linear models
- Define a decision tree
- Demonstrate how to estimate a decision tree
- Define and estimate a random forest
- Introduce the
caretpackage for statistical learning in R
Resampling methods
Resampling methods are essential to test and evaluate statistical models. Because you likely do not have the resources or capabilities to repeatedly sample from your population of interest, instead you can repeatedly draw from your original sample obtain additional information about your model. For instance, you could repeatedly draw samples from your data, estimate a linear regression model on each sample, and then examine how the estimated model differs across each sample. This allows you to assess the variability and stability of your model in a way not possible if you can only fit the model once.
Validation set
We have already seen the validation set approach in the previous class. By splitting our data into a training set and test set, we can evaluate the model’s effectiveness at predicting the response variable (in the context of either regression or classification) independently of the data used to estimate the model in the first place.
Classification
Recall how we used this approach to evaluate the accuracy of our interactive model predicting survival during the sinking of the Titanic.
titanic <- read_csv("data/titanic_train.csv")
titanic %>%
head() %>%
knitr::kable()| PassengerId | Survived | Pclass | Name | Sex | Age | SibSp | Parch | Ticket | Fare | Cabin | Embarked |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 3 | Braund, Mr. Owen Harris | male | 22 | 1 | 0 | A/5 21171 | 7.2500 | NA | S |
| 2 | 1 | 1 | Cumings, Mrs. John Bradley (Florence Briggs Thayer) | female | 38 | 1 | 0 | PC 17599 | 71.2833 | C85 | C |
| 3 | 1 | 3 | Heikkinen, Miss. Laina | female | 26 | 0 | 0 | STON/O2. 3101282 | 7.9250 | NA | S |
| 4 | 1 | 1 | Futrelle, Mrs. Jacques Heath (Lily May Peel) | female | 35 | 1 | 0 | 113803 | 53.1000 | C123 | S |
| 5 | 0 | 3 | Allen, Mr. William Henry | male | 35 | 0 | 0 | 373450 | 8.0500 | NA | S |
| 6 | 0 | 3 | Moran, Mr. James | male | NA | 0 | 0 | 330877 | 8.4583 | NA | Q |
survive_age_woman_x <- glm(Survived ~ Age * Sex, data = titanic,
family = binomial)
summary(survive_age_woman_x)##
## Call:
## glm(formula = Survived ~ Age * Sex, family = binomial, data = titanic)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -1.9401 -0.7136 -0.5883 0.7626 2.2455
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 0.59380 0.31032 1.913 0.05569 .
## Age 0.01970 0.01057 1.863 0.06240 .
## Sexmale -1.31775 0.40842 -3.226 0.00125 **
## Age:Sexmale -0.04112 0.01355 -3.034 0.00241 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 964.52 on 713 degrees of freedom
## Residual deviance: 740.40 on 710 degrees of freedom
## (177 observations deleted due to missingness)
## AIC: 748.4
##
## Number of Fisher Scoring iterations: 4logit2prob <- function(x){
exp(x) / (1 + exp(x))
}library(modelr)
titanic_split <- resample_partition(titanic, c(test = 0.3, train = 0.7))
map(titanic_split, dim)## $test
## [1] 267 12
##
## $train
## [1] 624 12train_model <- glm(Survived ~ Age + Sex, data = titanic_split$train,
family = binomial)
summary(train_model)##
## Call:
## glm(formula = Survived ~ Age + Sex, family = binomial, data = titanic_split$train)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -1.8433 -0.7331 -0.6742 0.7194 1.9246
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 1.514887 0.282736 5.358 8.42e-08 ***
## Age -0.009012 0.007550 -1.194 0.233
## Sexmale -2.475183 0.221260 -11.187 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 697.35 on 510 degrees of freedom
## Residual deviance: 543.50 on 508 degrees of freedom
## (113 observations deleted due to missingness)
## AIC: 549.5
##
## Number of Fisher Scoring iterations: 4x_test_accuracy <- titanic_split$test %>%
tbl_df() %>%
add_predictions(train_model) %>%
mutate(pred = logit2prob(pred),
pred = as.numeric(pred > .5))
mean(x_test_accuracy$Survived == x_test_accuracy$pred, na.rm = TRUE)## [1] 0.7931034Regression
This method also works for regression analysis. Here we will examine the relationship between horsepower and car mileage in the Auto dataset (found in library(ISLR)):
library(ISLR)
Auto <- Auto %>%
tbl_df()
Auto## # A tibble: 392 × 9
## mpg cylinders displacement horsepower weight acceleration year
## * <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 18 8 307 130 3504 12.0 70
## 2 15 8 350 165 3693 11.5 70
## 3 18 8 318 150 3436 11.0 70
## 4 16 8 304 150 3433 12.0 70
## 5 17 8 302 140 3449 10.5 70
## 6 15 8 429 198 4341 10.0 70
## 7 14 8 454 220 4354 9.0 70
## 8 14 8 440 215 4312 8.5 70
## 9 14 8 455 225 4425 10.0 70
## 10 15 8 390 190 3850 8.5 70
## # ... with 382 more rows, and 2 more variables: origin <dbl>, name <fctr>ggplot(Auto, aes(horsepower, mpg)) +
geom_point()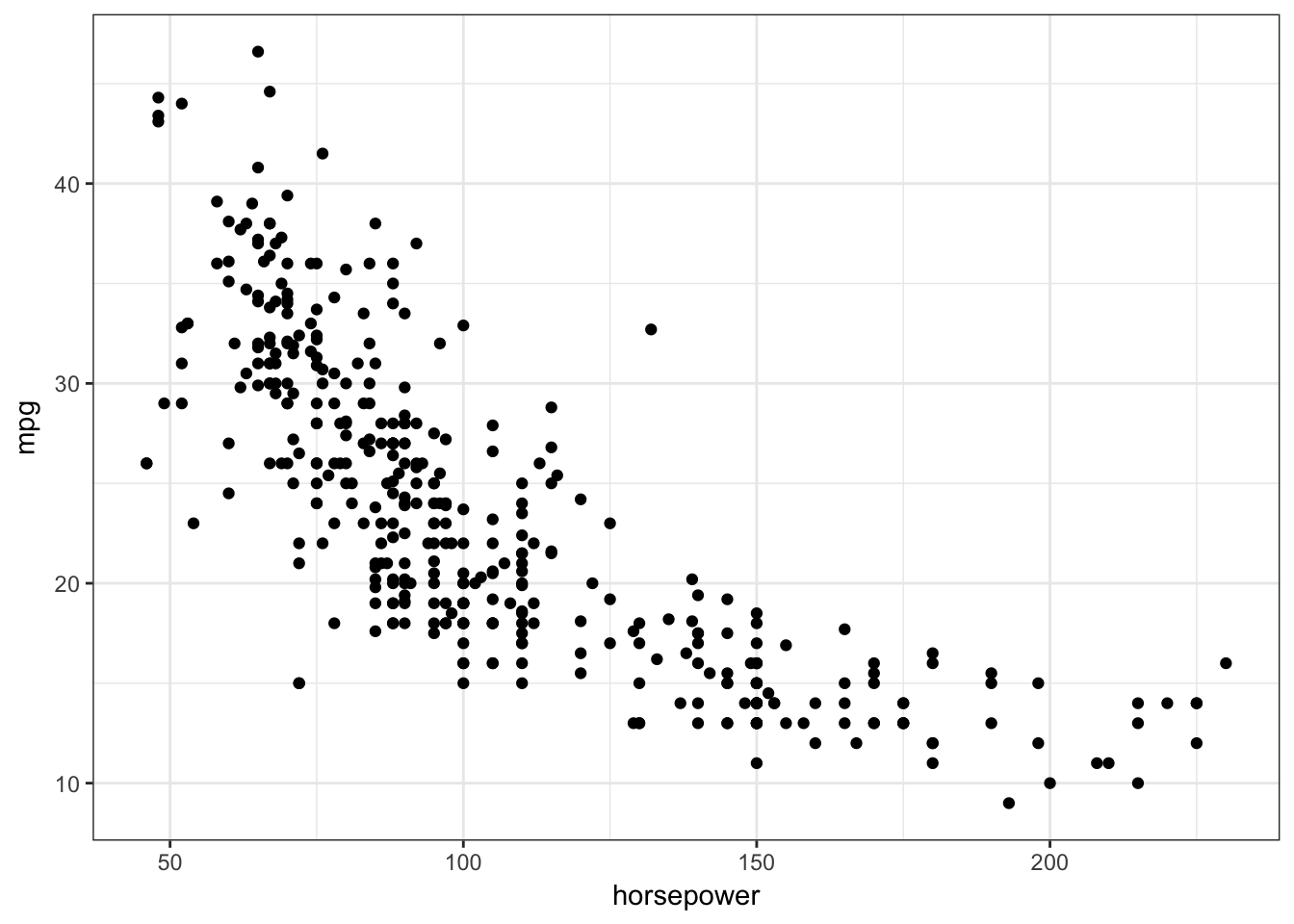
The relationship does not appear to be strictly linear:
ggplot(Auto, aes(horsepower, mpg)) +
geom_point() +
geom_smooth(method = "lm", se = FALSE)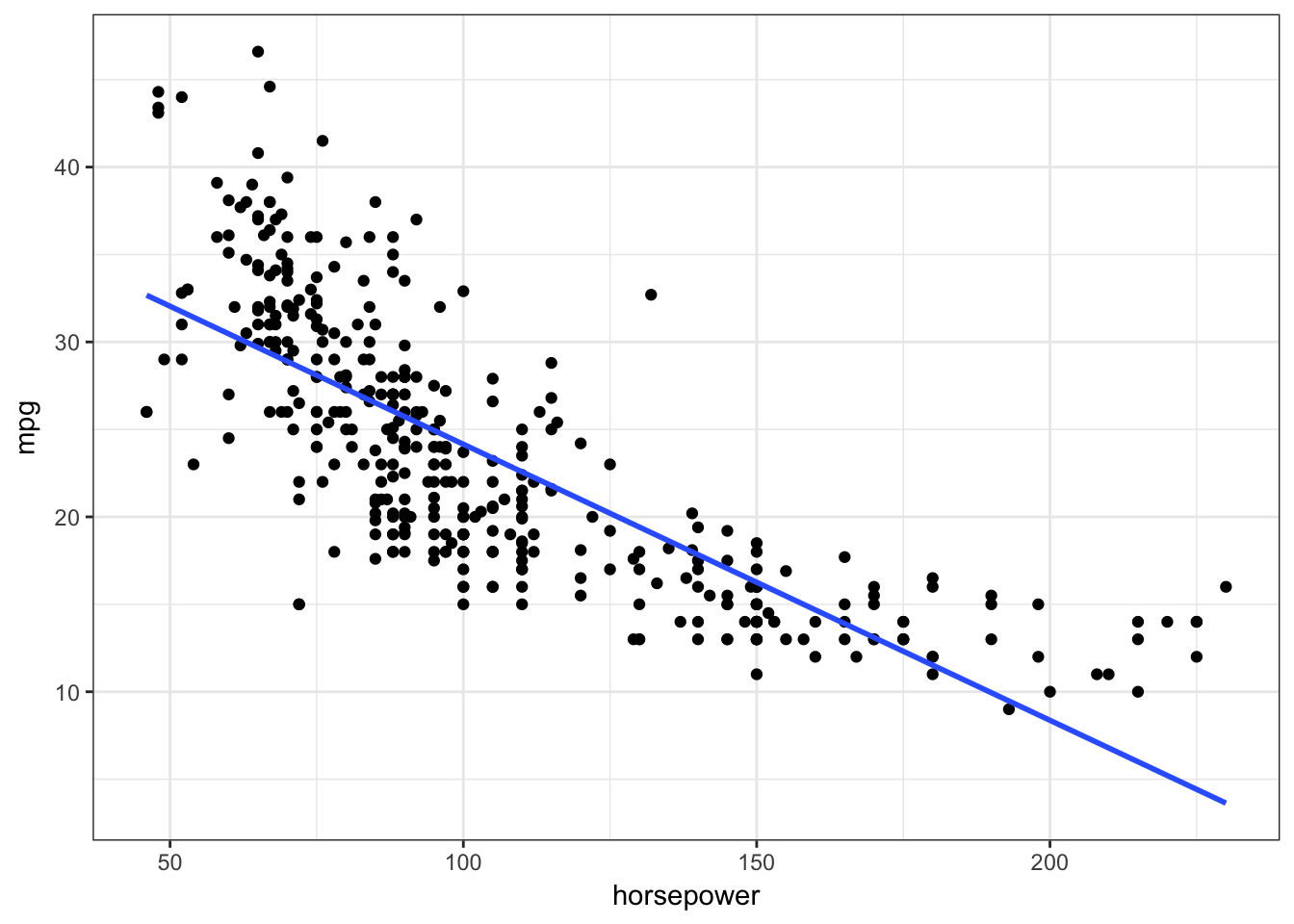
Perhaps by adding quadratic terms to the linear regression we could improve overall model fit. To evaluate the model, we will split the data into a training set and test set, estimate a series of higher-order models, and calculate a test statistic summarizing the accuracy of the estimated mpg. Rather than relying on the raw error rate (which makes sense in a classification model), we will instead use mean squared error (\(MSE\)), defined as
\[MSE = \frac{1}{n} \sum_{i = 1}^{n}{(y_i - \hat{f}(x_i))^2}\]
where:
- \(y_i =\) the observed response value for the \(i\)th observation
- \(\hat{f}(x_i) =\) the predicted response value for the \(i\)th observation given by \(\hat{f}\)
- \(n =\) the total number of observations
Boo math! Actually this is pretty intuitive. All we’re doing is for each observation, calculating the difference between the actual and predicted values for \(y\), squaring that difference, then calculating the average across all observations. An \(MSE\) of 0 indicates the model perfectly predicted each observation. The larger the \(MSE\), the more error in the model.
For this task, first we can use modelr::resample_partition to create training and test sets (using a 50/50 split), then estimate a linear regression model without any quadratic terms.
- I use
set.seed()in the beginning - whenever you are writing a script that involves randomization (here, random subsetting of the data), always set the seed at the beginning of the script. This ensures the results can be reproduced precisely.1 - I also use the
glmfunction rather thanlm- if you don’t change thefamilyparameter, the results oflmandglmare exactly the same. I do this because I want to use a cross-validation function later that only works with results from aglmfunction.
set.seed(1234)
auto_split <- resample_partition(Auto, c(test = 0.5, train = 0.5))
auto_train <- auto_split$train %>%
tbl_df()
auto_test <- auto_split$test %>%
tbl_df()auto_lm <- glm(mpg ~ horsepower, data = auto_train)
summary(auto_lm)##
## Call:
## glm(formula = mpg ~ horsepower, data = auto_train)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -12.892 -2.864 -0.545 2.793 13.298
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 38.005404 0.921129 41.26 <2e-16 ***
## horsepower -0.140459 0.007968 -17.63 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for gaussian family taken to be 20.48452)
##
## Null deviance: 10359.4 on 196 degrees of freedom
## Residual deviance: 3994.5 on 195 degrees of freedom
## AIC: 1157.9
##
## Number of Fisher Scoring iterations: 2To estimate the \(MSE\), I write a brief function that requires two inputs: the dataset and the linear model.2
MSE_mpg <- function(model, data){
mean((predict(model, data) - data$mpg)^2)
}
MSE_mpg(auto_lm, auto_test)## [1] 28.57255For a strictly linear model, the \(MSE\) for the test set is 28.57. How does this compare to a quadratic model? We can use the poly function in conjunction with a map iteration to estimate the \(MSE\) for a series of models with higher-order polynomial terms:
auto_poly <- function(i){
glm(mpg ~ poly(horsepower, i), data = auto_train)
}
auto_poly_results <- data_frame(terms = 1:5,
model = map(terms, auto_poly),
MSE = map_dbl(model, MSE_mpg, data = auto_test))
ggplot(auto_poly_results, aes(terms, MSE)) +
geom_line() +
labs(title = "Comparing quadratic linear models",
subtitle = "Using validation set",
x = "Highest-order polynomial",
y = "Mean Squared Error")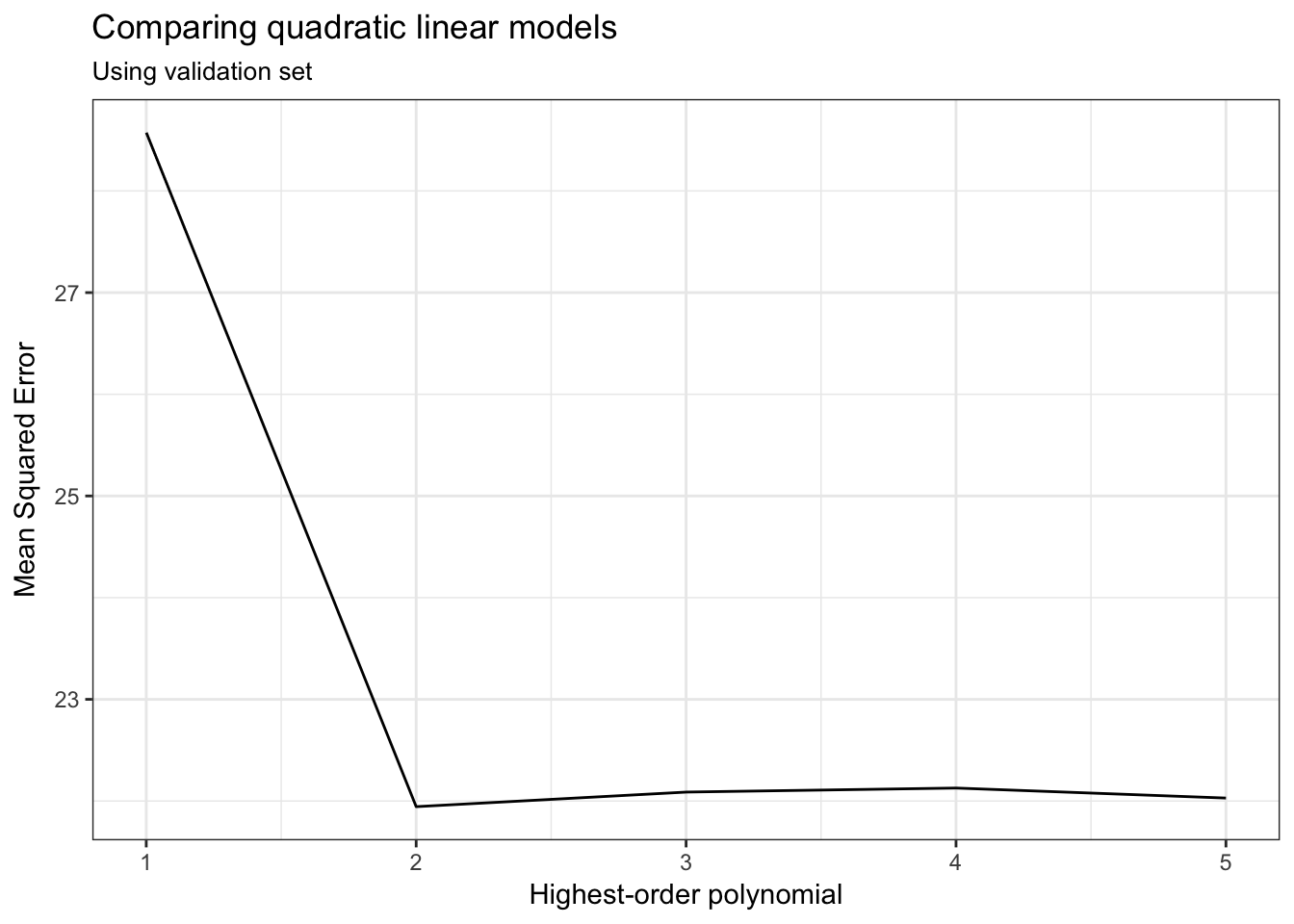
Based on the \(MSE\) for the validation (test) set, a polynomial model with a quadratic term (\(\text{horsepower}^2\)) produces the lowest average error. Adding cubic or higher-order terms is just not necessary.
Drawbacks to validation sets
There are two main problems with validation sets:
Validation estimates of the test error rates can be highly variable depending on which observations are sampled into the training and test sets. See what happens if we repeat the sampling, estimation, and validation procedure for the
Autodata set:mse_variable <- function(Auto){ auto_split <- resample_partition(Auto, c(test = 0.5, train = 0.5)) auto_train <- auto_split$train %>% tbl_df() auto_test <- auto_split$test %>% tbl_df() auto_poly <- function(i){ glm(mpg ~ poly(horsepower, i), data = auto_train) } results <- data_frame(terms = 1:5, model = map(terms, auto_poly), MSE = map_dbl(model, MSE_mpg, data = auto_test)) return(results) } rerun(10, mse_variable(Auto)) %>% bind_rows(.id = "id") %>% ggplot(aes(terms, MSE, color = id)) + geom_line() + labs(title = "Variability of MSE estimates", subtitle = "Using the validation set approach", x = "Degree of Polynomial", y = "Mean Squared Error") + theme(legend.position = "none")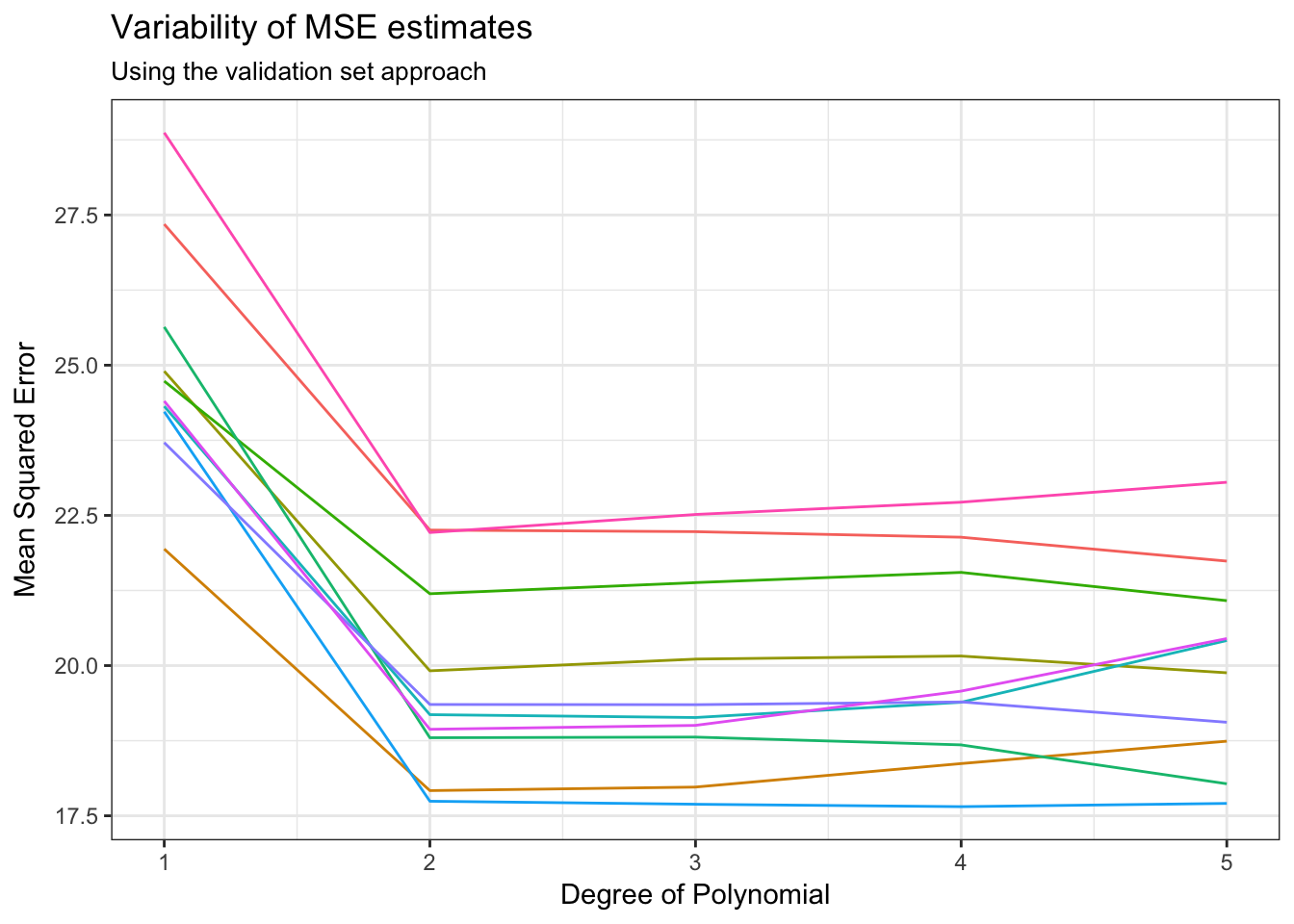
If you don’t have a large data set, you’ll have to dramatically shrink the size of your training set. Most statistical learning methods perform better with more observations - if you don’t have enough data in the training set, you might overestimate the error rate in the test set.
Leave-one-out cross-validation
An alternative method is leave-one-out cross validation (LOOCV). Like with the validation set approach, you split the data into two parts. However the difference is that you only remove one observation for the test set, and keep all remaining observations in the training set. The statistical learning method is fit on the \(n-1\) training set. You then use the held-out observation to calculate the \(MSE = (y_1 - \hat{y}_1)^2\) which should be an unbiased estimator of the test error. Because this \(MSE\) is highly dependent on which observation is held out, we repeat this process for every single observation in the data set. Mathematically, this looks like:
\[CV_{(n)} = \frac{1}{n} \sum_{i = 1}^{n}{MSE_i}\]
This method produces estimates of the error rate that have minimal bias and relatively steady (i.e. non-varying), unlike the validation set approach where the \(MSE\) estimate is highly dependent on the sampling process for training/test sets. LOOCV is also highly flexible and works with any kind of predictive modeling.
Of course the downside is that this method is computationally difficult. You have to estimate \(n\) different models - if you have a large \(n\) or each individual model takes a long time to compute, you may be stuck waiting a long time for the computer to finish its calculations.
LOOCV in linear regression
We can use the cv.glm function in the boot library to compute the LOOCV of any linear or logistic regression model. For the Auto dataset, this looks like:
library(boot)
auto_lm <- glm(mpg ~ horsepower, data = Auto)
auto_lm_err <- cv.glm(Auto, auto_lm)
auto_lm_err$delta[1]## [1] 24.23151cv.glm produces a list with several components. The two numbers in the delta vector contain the results of the LOOCV. The first number is what we care about the most, and is the LOOCV estimate of the \(MSE\) for the dataset.
We can also use this method to compare the optimal number of polynomial terms as before.
cv_error <- vector("numeric", 5)
terms <- 1:5
for(i in terms){
glm_fit <- glm(mpg ~ poly(horsepower, i), data = Auto)
cv_error[[i]] <- cv.glm(Auto, glm_fit)$delta[[1]]
}
cv_mse <- data_frame(terms = terms,
cv_MSE = cv_error)
cv_mse## # A tibble: 5 × 2
## terms cv_MSE
## <int> <dbl>
## 1 1 24.23151
## 2 2 19.24821
## 3 3 19.33498
## 4 4 19.42443
## 5 5 19.03321ggplot(cv_mse, aes(terms, cv_MSE)) +
geom_line() +
labs(title = "Comparing quadratic linear models",
subtitle = "Using LOOCV",
x = "Highest-order polynomial",
y = "Mean Squared Error")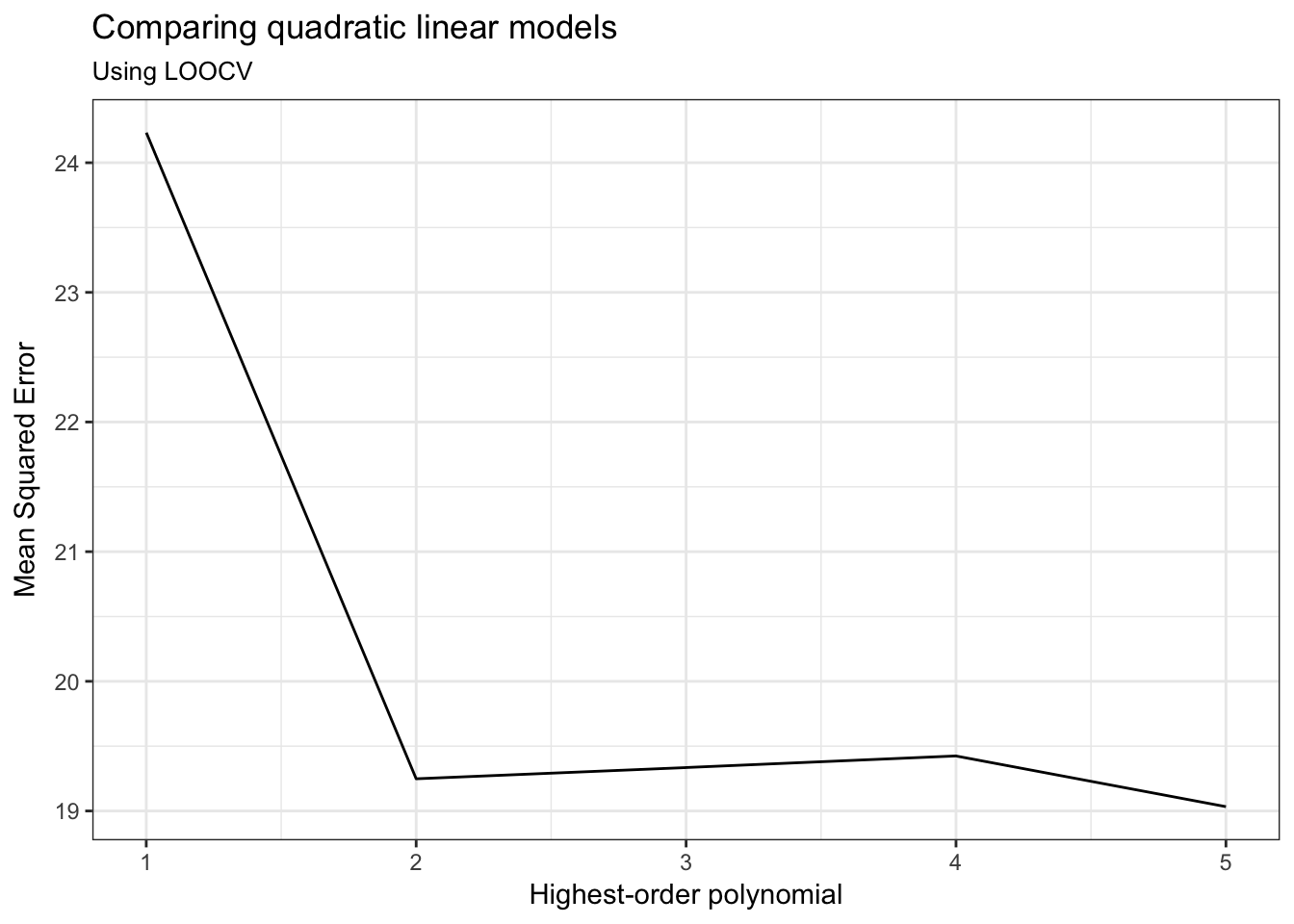
And arrive at the same conclusion.
LOOCV in classification
Let’s use classification to validate the interactive terms model from before. Before we can estimate the LOOCV, we need to first remove any observations from titanic which have missing values for Survived, Age, or Sex (glm does this for us automatically, whereas cv.glm does not. And since cv.glm requires the data frame as its first argument, we can use the pipe %>%):
titanic_model <- glm(Survived ~ Age * Sex, data = titanic,
family = binomial)
titanic_loocv <- titanic %>%
filter(!is.na(Survived), !is.na(Age), !is.na(Sex)) %>%
cv.glm(titanic_model)
titanic_loocv$delta[[1]]## [1] 0.1703518In a classification problem, the LOOCV tells us the average error rate based on our predictions. So here, it tells us that the interactive Age * Sex model has a 17% error rate. This is similar to the validation set result (\(79.3\%\))
k-fold cross-validation
A less computationally-intensive approach to cross validation is \(k\)-fold cross-validation. Rather than dividing the data into \(n\) groups, one divides the observations into \(k\) groups, or folds, of approximately equal size. The first fold is treated as the validation set, the model is estimated on the remaining \(k-1\) folds. This process is repeated \(k\) times, with each fold serving as the validation set precisely once. The \(k\)-fold CV estimate is calculated by averaging the \(MSE\) values for each fold:
\[CV_{(k)} = \frac{1}{k} \sum_{i = 1}^{k}{MSE_i}\]
LOOCV is the special case of \(k\)-fold cross-validation where \(k = n\). More typically researchers will use \(k=5\) or \(k=10\) depending on the size of the data set and the complexity of the statistical model.
k-fold CV in linear regression
Let’s go back to the Auto data set. Instead of LOOCV, let’s use 10-fold CV to compare the different polynomial models.
cv_error_fold10 <- vector("numeric", 5)
terms <- 1:5
for(i in terms){
glm_fit <- glm(mpg ~ poly(horsepower, i), data = Auto)
cv_error_fold10[[i]] <- cv.glm(Auto, glm_fit, K = 10)$delta[[1]]
}
cv_error_fold10## [1] 24.42374 19.28760 19.20702 19.42017 18.96962How do these results compare to the LOOCV values?
data_frame(terms = terms,
loocv = cv_error,
fold10 = cv_error_fold10) %>%
gather(method, MSE, loocv:fold10) %>%
ggplot(aes(terms, MSE, color = method)) +
geom_line() +
labs(title = "MSE estimates",
x = "Degree of Polynomial",
y = "Mean Squared Error",
color = "CV Method")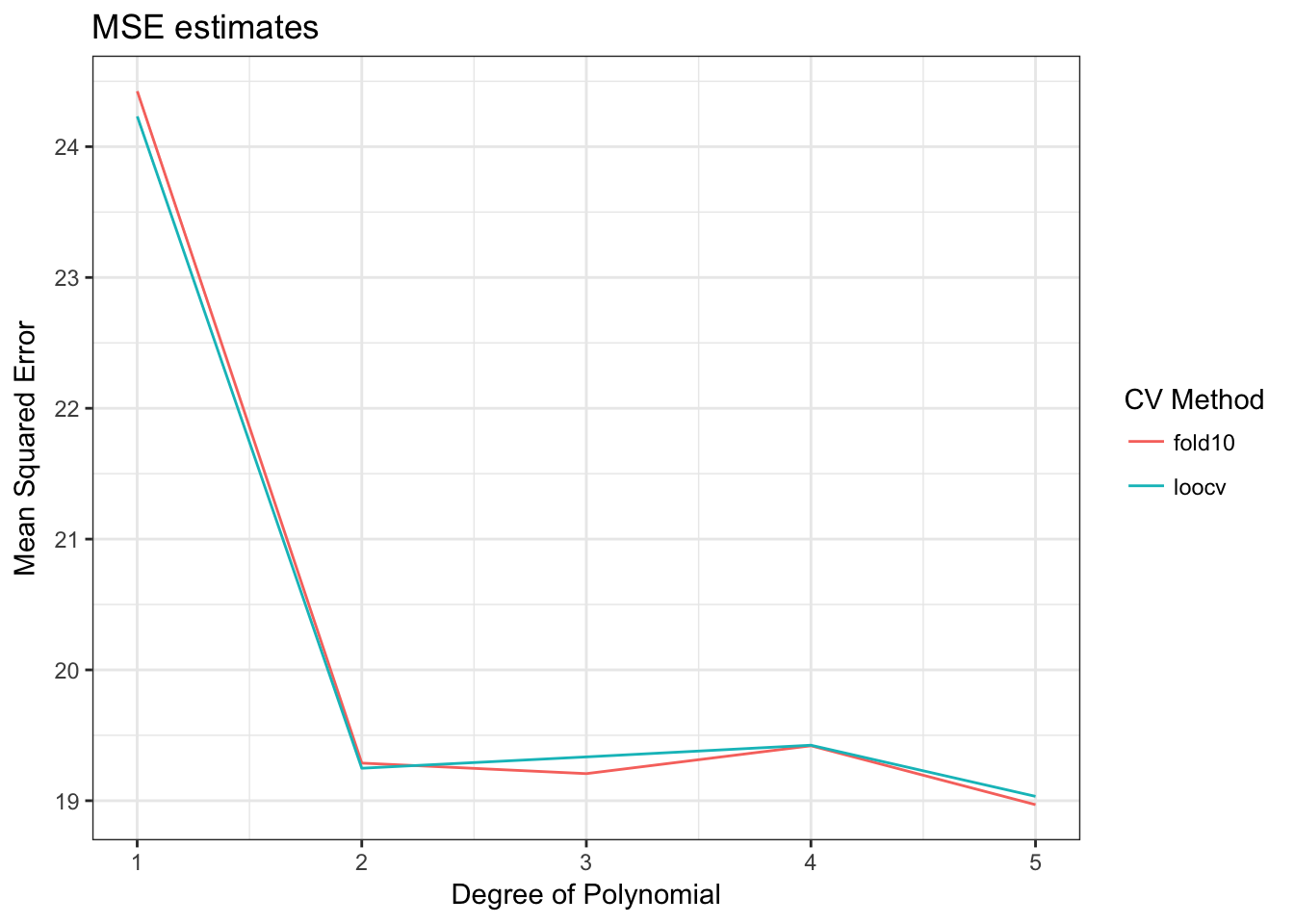
Pretty much the same results. But computationally, how long does it take to estimate the 10-fold CV versus LOOCV? We can use the profvis package to profile our code and determine how long it takes to run.
LOOCV
library(profvis)
profvis({
cv_error <- vector("numeric", 5)
terms <- 1:5
for (i in terms) {
glm_fit <- glm(mpg ~ poly(horsepower, i), data = Auto)
cv_error[[i]] <- cv.glm(Auto, glm_fit)$delta[[1]]
}
})10-fold CV
library(profvis)
profvis({
cv_error_fold10 <- vector("numeric", 5)
terms <- 1:5
for (i in terms) {
glm_fit <- glm(mpg ~ poly(horsepower, i), data = Auto)
cv_error_fold10[[i]] <- cv.glm(Auto, glm_fit, K = 10)$delta[[1]]
}
})On my machine, 10-fold CV was about 40 times faster than LOOCV. Again, estimating \(k=10\) models is going to be much easier than estimating \(k=392\) models.
k-fold CV in logistic regression
You’ve gotten the idea by now, but let’s do it one more time on our interactive Titanic model.
titanic_kfold <- titanic %>%
filter(!is.na(Survived), !is.na(Age), !is.na(Sex)) %>%
cv.glm(titanic_model, K = 10)
titanic_kfold$delta[[1]]## [1] 0.1708052Not a large difference from the LOOCV approach, but it take much less time to compute.
Decision trees


Decision trees are intuitive concepts for making decisions. They are also useful methods for regression and classification. They work by splitting the observations into a number of regions, and predictions are made based on the mean or mode of the training observations in that region.
Interpreting a decision tree
Let’s start with the Titanic data. I want to predict who lives and who dies during this event. Instead of using logistic regression, I’m going to calculate a decision tree based on a passenger’s age and gender. Here’s what that decision tree looks like:
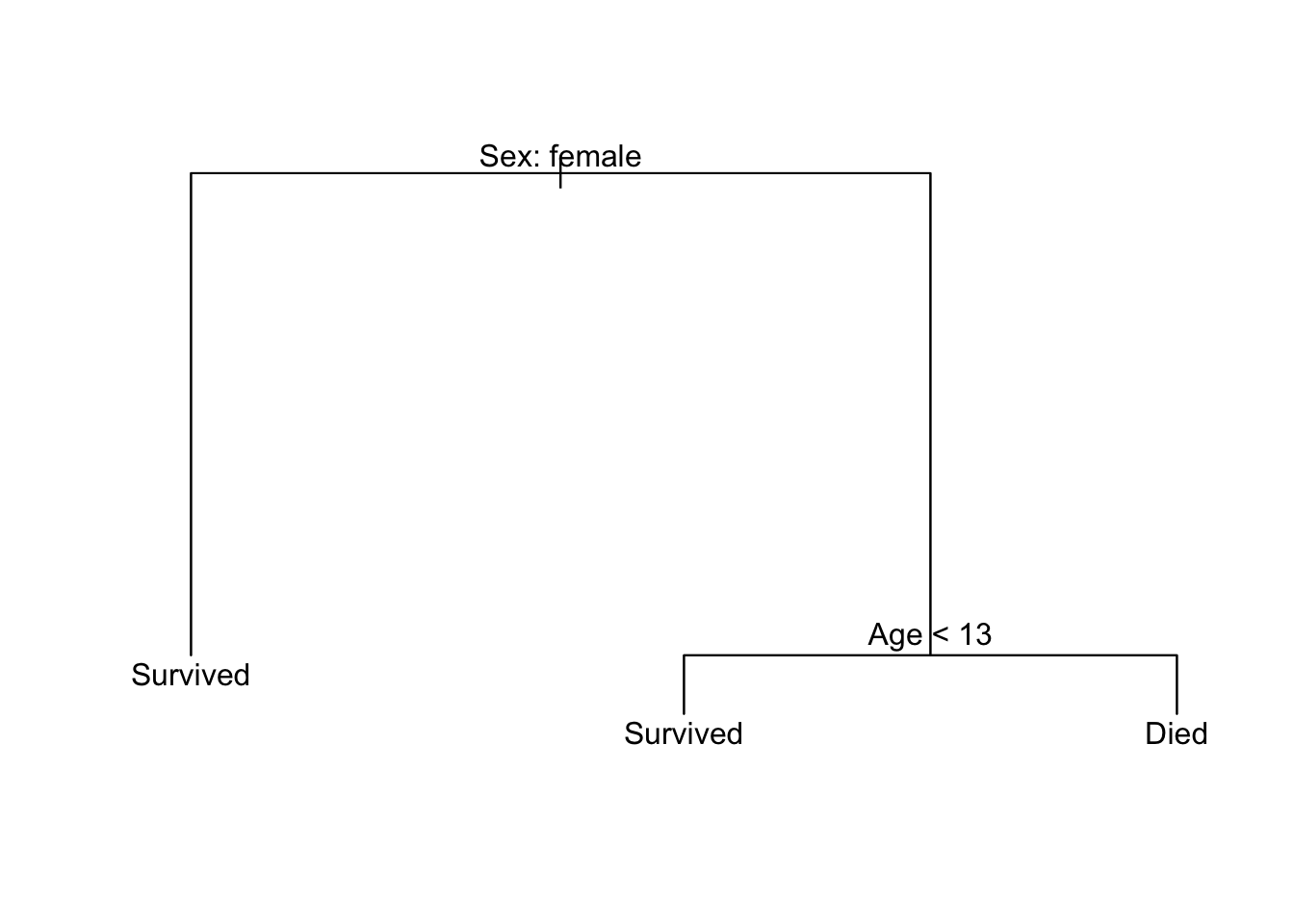
Some key terminology:
- Each outcome (survived or died) is a terminal node or a leaf
- Splits occur at internal nodes
- The segments connecting each node are called branches
To make a prediction for a specific passenger, we start the decision tree from the top node and follow the appropriate branches down until we reach a terminal node. At each internal node, if our observation matches the condition, then travel down the left branch. If our observation does not match the condition, then travel down the right branch.
So for a 50 year old female passenger:
- Start at the first internal node. The passenger in question is a female, so take the branch to the left.
- We reach a terminal node (“Survived”). We would predict the passenger in question survived the sinking of the Titanic.
For a 20 year old male passenger:
- Start at the first internal node - the passenger in question is a male, so take the branch to the right.
- The passenger in question is not less than 13 years old (R would say the condition is
FALSE), so take the branch to the right. - We reach a terminal node (“Died”). We would predict the passenger in question died in the sinking of the Titanic.
Estimating a decision tree
First we need to load the tree library and prepare the data. tree is somewhat finicky about how data must be formatted in order to estimate the tree. For the Titanic data, we need to convert all qualitiative variables to factors using the as.factor function. To make interpretation easier, I also recode Survived from its 0/1 coding to explicitly identify which passengers survived and which died.
library(tree)
titanic_tree_data <- titanic %>%
mutate(Survived = ifelse(Survived == 1, "Survived",
ifelse(Survived == 0, "Died", NA)),
Survived = as.factor(Survived),
Sex = as.factor(Sex))
titanic_tree_data## # A tibble: 891 × 12
## PassengerId Survived Pclass
## <int> <fctr> <int>
## 1 1 Died 3
## 2 2 Survived 1
## 3 3 Survived 3
## 4 4 Survived 1
## 5 5 Died 3
## 6 6 Died 3
## 7 7 Died 1
## 8 8 Died 3
## 9 9 Survived 3
## 10 10 Survived 2
## # ... with 881 more rows, and 9 more variables: Name <chr>, Sex <fctr>,
## # Age <dbl>, SibSp <int>, Parch <int>, Ticket <chr>, Fare <dbl>,
## # Cabin <chr>, Embarked <chr>Now we can use the tree function to estimate the model. The format looks exactly like lm or glm - first we specify the formula that defines the model, then we specify where the data is stored:
titanic_tree <- tree(Survived ~ Age + Sex, data = titanic_tree_data)
summary(titanic_tree)##
## Classification tree:
## tree(formula = Survived ~ Age + Sex, data = titanic_tree_data)
## Number of terminal nodes: 3
## Residual mean deviance: 1.019 = 724.7 / 711
## Misclassification error rate: 0.2129 = 152 / 714The summary function provides several important statistics:
- There are three terminal nodes in the tree
- Residual mean deviance is an estimate of model fit. It is usually helpful in comparing the effectiveness of different models.
- This decision tree misclassifies \(21.3\%\) of the training set observations (note that we did not create a validation set - this model is based on all the original data)
That’s all well in good, but decision trees are meant to be viewed. Let’s plot it!
plot(titanic_tree)
text(titanic_tree, pretty = 0)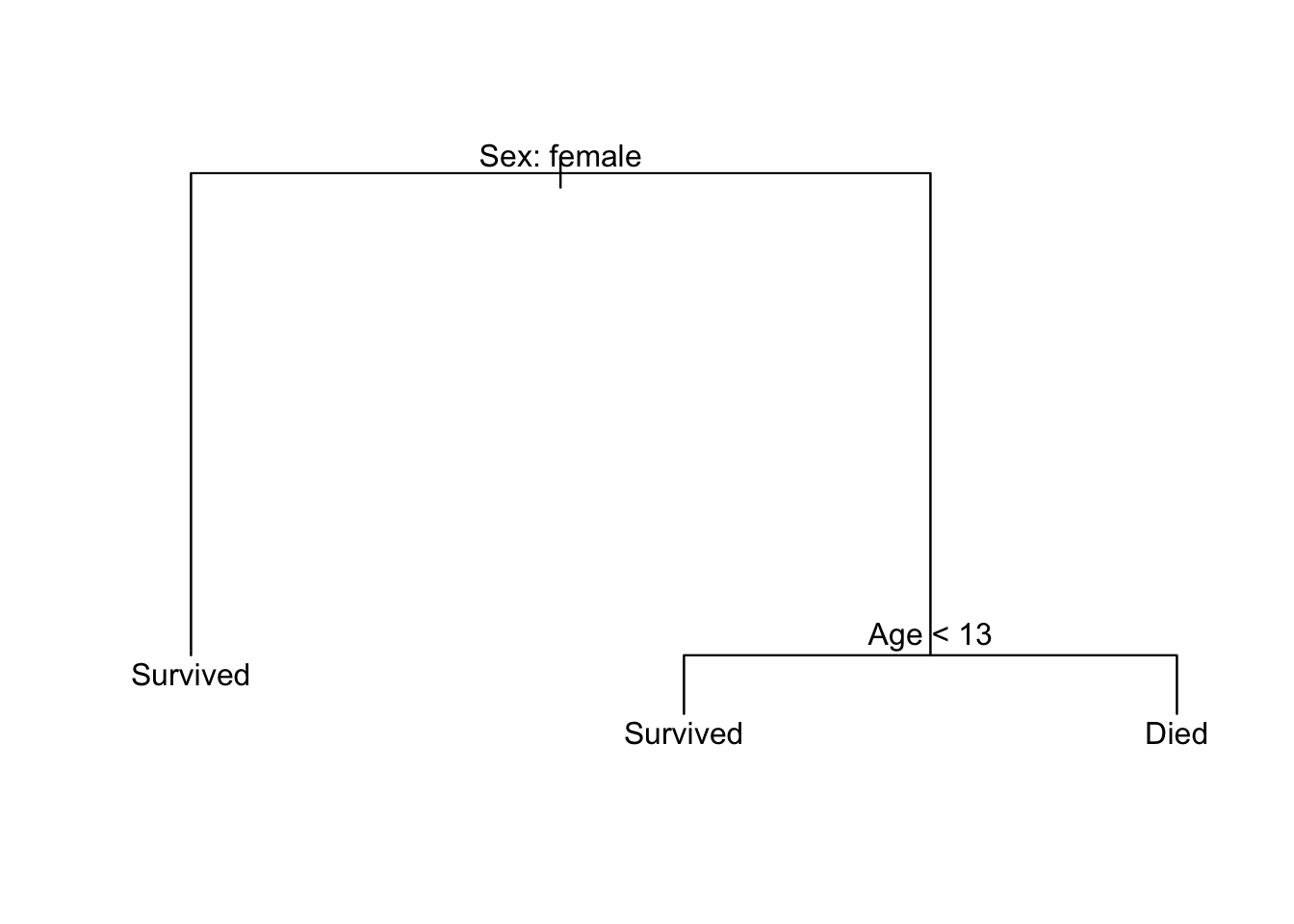
tree does not use ggplot2 to graph the results; instead it relies on the base graphics package. plot(titanic_tree) draws the branches and text(titanic_tree, pretty = 0) adds the text labeling each node.3
Build a more complex tree
Since we have a lot of other variables in our Titanic data set, let’s estimate a more complex model that accounts for all the information we have.4 We’ll have to format all our columns this time before we can estimate the model. Because there are multiple qualitative variables as predictors, I will use mutate_each to apply as.factor to all of these variables in one line of code (another type of iterative operation):
titanic_tree_full_data <- titanic %>%
mutate(Survived = ifelse(Survived == 1, "Survived",
ifelse(Survived == 0, "Died", NA))) %>%
mutate_each(funs(as.factor), Survived, Pclass, Sex, Embarked)
titanic_tree_full <- tree(Survived ~ Pclass + Sex + Age + SibSp +
Parch + Fare + Embarked, data = titanic_tree_full_data)
summary(titanic_tree_full)##
## Classification tree:
## tree(formula = Survived ~ Pclass + Sex + Age + SibSp + Parch +
## Fare + Embarked, data = titanic_tree_full_data)
## Variables actually used in tree construction:
## [1] "Sex" "Pclass" "Fare" "Age" "SibSp"
## Number of terminal nodes: 7
## Residual mean deviance: 0.7995 = 563.6 / 705
## Misclassification error rate: 0.1742 = 124 / 712plot(titanic_tree_full)
text(titanic_tree_full, pretty = 0)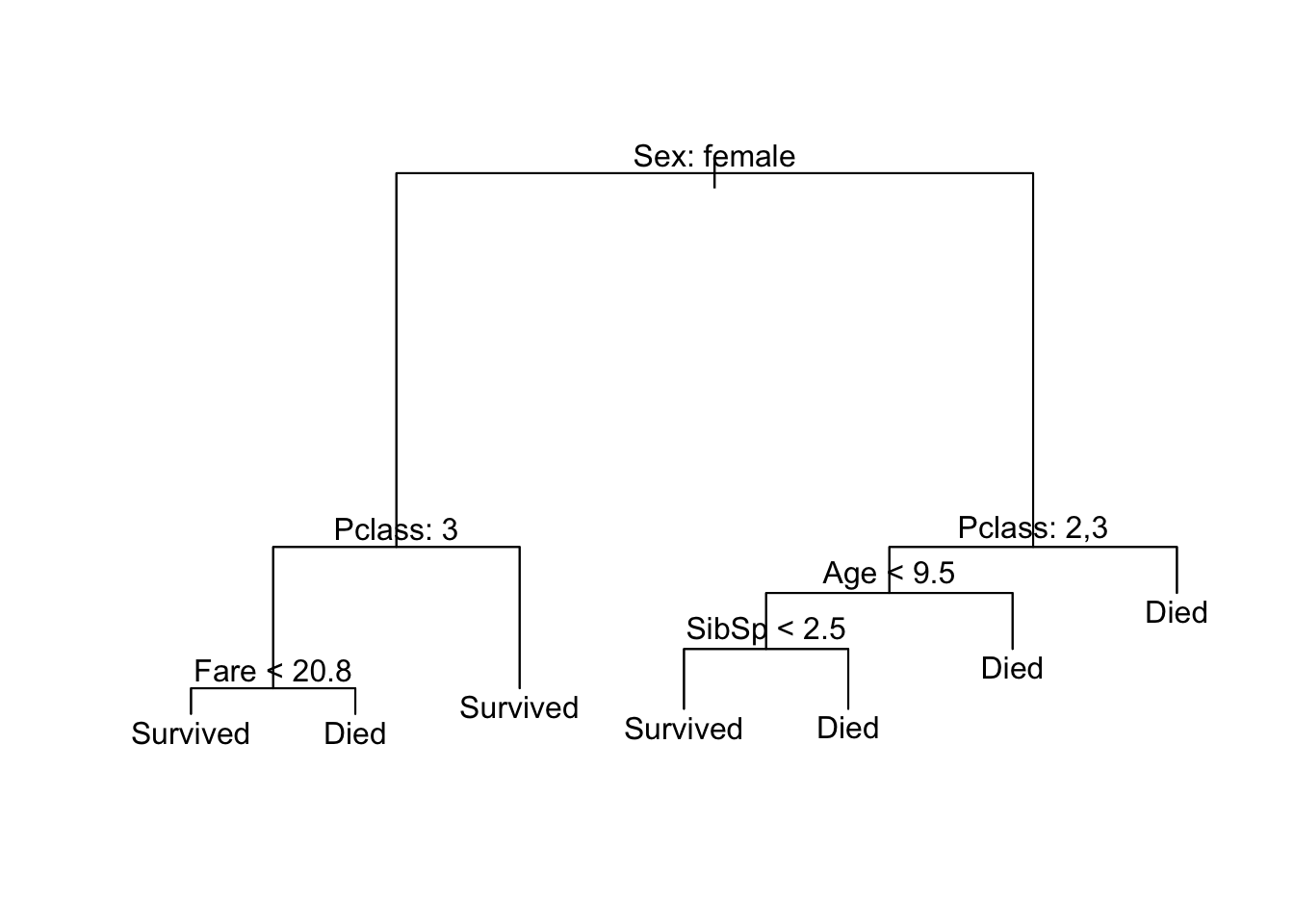
Now we’ve built a more complicated decision tree. Fortunately it is still pretty interpretable. Notice that some of the variables we included in the model (Parch and Embarked) ended up being dropped from the final model. This is because to build the tree and ensure it is not overly complicated, the algorithm goes through a process of iteration and pruning to remove twigs or branches that result in a complicated model that does not provide significant improvement in overall model accuracy. You can tweak these parameters to ensure the model keeps all the variables, but could result in a nasty looking picture:
titanic_tree_messy <- tree(Survived ~ Pclass + Sex + Age + SibSp +
Parch + Fare + Embarked,
data = titanic_tree_full_data,
control = tree.control(nobs = nrow(titanic_tree_full_data),
mindev = 0, minsize = 10))
summary(titanic_tree_messy)##
## Classification tree:
## tree(formula = Survived ~ Pclass + Sex + Age + SibSp + Parch +
## Fare + Embarked, data = titanic_tree_full_data, control = tree.control(nobs = nrow(titanic_tree_full_data),
## mindev = 0, minsize = 10))
## Number of terminal nodes: 76
## Residual mean deviance: 0.5164 = 328.4 / 636
## Misclassification error rate: 0.1124 = 80 / 712plot(titanic_tree_messy)
text(titanic_tree_messy, pretty = 0)
The misclassification error rate for this model is much lower than the previous versions, but it is also much less interpretable. Depending on your audience and how you want to present the results of your statistical model, you need to determine the optimal trade-off between accuracy and interpretability.
Benefits/drawbacks to decision trees
Decision trees are an entirely different method of estimating functional forms as compared to linear regression. There are some benefits to trees:
- They are easy to explain. Most people, even if they lack statistical training, can understand decision trees.
- They are easily presented as visualizations, and pretty interpretable.
- Qualitative predictors are easily handled without the need to create a long series of dummy variables.
However there are also drawbacks to trees:
- Their accuracy rates are generally lower than other regression and classification approaches.
- Trees can be non-robust. That is, a small change in the data or inclusion/exclusion of a handful of observations can dramatically alter the final estimated tree.
Fortuntately, there is an easy way to improve on these poor predictions: by aggregating many decision trees and averaging across them, we can substantially improve performance.
Random forests
One method of aggregating trees is the random forest approach. This uses the concept of bootstrapping build a forest of trees using the same underlying data set. Bootstrapping is standard resampling process whereby you repeatedly sample with replacement from a data set. So if you have a dataset of 500 observations, you might draw a sample of 500 observations from the data. But by sampling with replacement, some observations may be sampled multiple times and some observations may never be sampled. This essentially treats your data as a population of interest. You repeat this process many times (say 1000), then estimate your quantity or model of interest on each sample. Then finally you average across all the bootstrapped samples to calculate the final model or statistical estimator.
As with other resampling methods, each individual sample will have some degree of bias to it. However by averaging across all the bootstrapped samples you cancel out much of this bias. Most importantly, averaging a set of observations reduces variance - this is what LOOCV and \(k\)-fold cross-validation do. You achieve stable estimates of the prediction accuracy or overall model error.
In the context of decision trees, this means we draw repeated samples from the original dataset and estimate a decision tree model on each sample. To make predictions, we estimate the outcome using each tree and average across all of them to obtain the final prediction. Rather than being a binary outcome (\([0,1]\), survived/died), the average prediction will be a probability of the given outcome (i.e. the probability of survival). This process is called bagging. Random forests go a step further: when building individual decision trees, each time a split in the tree is considered a random sample of predictors is selected as the candidates for the split. Random forests specifically exclude a portion of the predictor variables when building individual trees. Why throw away good data? This ensures each decision tree is not correlated with one another. If one specific variable was a strong predictor in the data set (say gender in the Titanic data set), it could potentially dominate every decision tree and the result would be nearly-identical trees regardless of the sampling procedure. By forcibly excluding a random subset of variables, individual trees in random forests will not have strong correlations with one another. Therefore the average predictions will be more reliable.
Estimating statistical models using caret
To estimate a random forest, we move outside the world of tree and into a new package in R: caret. caret is a package in R for training and plotting a wide variety of statistical learning models. It is outside of the tidyverse so can be a bit more difficult to master. caret does not contain the estimation algorithms itself; instead it creates a unified interface to approximately 233 different models from various packages in R. To install caret and make sure you install all the related packages it relies on, run the following code:
install.packages("caret", dependencies = TRUE)The basic function to train models is train. We can train regression and classification models using one of these models. For instance, rather than using glm to estimate a logistic regression model, we could use caret and the "glm" method instead. Note that caret is extremely picky about preparing data for analysis. For instance, we have to remove all missing values before training a model.
library(caret)
titanic_clean <- titanic %>%
filter(!is.na(Survived), !is.na(Age))
caret_glm <- train(Survived ~ Age, data = titanic_clean,
method = "glm",
family = binomial,
trControl = trainControl(method = "none"))
summary(caret_glm)##
## Call:
## NULL
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -1.1488 -1.0361 -0.9544 1.3159 1.5908
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -0.05672 0.17358 -0.327 0.7438
## Age -0.01096 0.00533 -2.057 0.0397 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 964.52 on 713 degrees of freedom
## Residual deviance: 960.23 on 712 degrees of freedom
## AIC: 964.23
##
## Number of Fisher Scoring iterations: 4trControl = trainControl(method = "none")- by defaultcaretimplements a bootstrap resampling procedure to validate the results of the model. For our purposes here I want to turn that off by setting the resampling method to"none".
The results are identical to those obtained by the glm function:5
glm_glm <- glm(Survived ~ Age, data = titanic_clean, family = "binomial")
summary(glm_glm)##
## Call:
## glm(formula = Survived ~ Age, family = "binomial", data = titanic_clean)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -1.1488 -1.0361 -0.9544 1.3159 1.5908
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -0.05672 0.17358 -0.327 0.7438
## Age -0.01096 0.00533 -2.057 0.0397 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 964.52 on 713 degrees of freedom
## Residual deviance: 960.23 on 712 degrees of freedom
## AIC: 964.23
##
## Number of Fisher Scoring iterations: 4Estimating a random forest
We will reuse titanic_tree_full_data with the adjustment that we need to remove observations with missing values. In the process, let’s pare the data frame down to only columns that will be used the model:
titanic_rf_data <- titanic_tree_full_data %>%
select(Survived, Pclass, Sex, Age, SibSp, Parch, Fare, Embarked) %>%
na.omit()
titanic_rf_data## # A tibble: 712 × 8
## Survived Pclass Sex Age SibSp Parch Fare Embarked
## <fctr> <fctr> <fctr> <dbl> <int> <int> <dbl> <fctr>
## 1 Died 3 male 22 1 0 7.2500 S
## 2 Survived 1 female 38 1 0 71.2833 C
## 3 Survived 3 female 26 0 0 7.9250 S
## 4 Survived 1 female 35 1 0 53.1000 S
## 5 Died 3 male 35 0 0 8.0500 S
## 6 Died 1 male 54 0 0 51.8625 S
## 7 Died 3 male 2 3 1 21.0750 S
## 8 Survived 3 female 27 0 2 11.1333 S
## 9 Survived 2 female 14 1 0 30.0708 C
## 10 Survived 3 female 4 1 1 16.7000 S
## # ... with 702 more rowsNow that the data is prepped, let’s estimate the model. To start, we’ll estimate a simple model that only uses age and gender. Again we use the train function but this time we will use the rf method.6 To start with, I will estimate a forest with 200 trees (the default is 500 trees) and set the trainControl method to "oob" (I will explain this shortly):
age_sex_rf <- train(Survived ~ Age + Sex, data = titanic_rf_data,
method = "rf",
ntree = 200,
trControl = trainControl(method = "oob"))## note: only 1 unique complexity parameters in default grid. Truncating the grid to 1 .age_sex_rf## Random Forest
##
## 712 samples
## 2 predictor
## 2 classes: 'Died', 'Survived'
##
## No pre-processing
## Resampling results:
##
## Accuracy Kappa
## 0.7598315 0.4938641
##
## Tuning parameter 'mtry' was held constant at a value of 2
## Hmm. What have we generated here? How can we analyze the results?
Structure of train object
The object generated by train is a named list:
str(age_sex_rf, max.level = 1)## List of 24
## $ method : chr "rf"
## $ modelInfo :List of 15
## $ modelType : chr "Classification"
## $ results :'data.frame': 1 obs. of 3 variables:
## $ pred : NULL
## $ bestTune :'data.frame': 1 obs. of 1 variable:
## $ call : language train.formula(form = Survived ~ Age + Sex, data = titanic_rf_data, method = "rf", ntree = 200, trControl = trainControl(method = "oob"))
## $ dots :List of 1
## $ metric : chr "Accuracy"
## $ control :List of 26
## $ finalModel :List of 22
## ..- attr(*, "class")= chr "randomForest"
## $ preProcess : NULL
## $ trainingData:Classes 'tbl_df', 'tbl' and 'data.frame': 712 obs. of 3 variables:
## $ resample : NULL
## $ resampledCM : NULL
## $ perfNames : chr [1:2] "Accuracy" "Kappa"
## $ maximize : logi TRUE
## $ yLimits : NULL
## $ times :List of 3
## $ levels : atomic [1:2] Died Survived
## ..- attr(*, "ordered")= logi FALSE
## $ terms :Classes 'terms', 'formula' language Survived ~ Age + Sex
## .. ..- attr(*, "variables")= language list(Survived, Age, Sex)
## .. ..- attr(*, "factors")= int [1:3, 1:2] 0 1 0 0 0 1
## .. .. ..- attr(*, "dimnames")=List of 2
## .. ..- attr(*, "term.labels")= chr [1:2] "Age" "Sex"
## .. ..- attr(*, "order")= int [1:2] 1 1
## .. ..- attr(*, "intercept")= int 1
## .. ..- attr(*, "response")= int 1
## .. ..- attr(*, ".Environment")=<environment: R_GlobalEnv>
## .. ..- attr(*, "predvars")= language list(Survived, Age, Sex)
## .. ..- attr(*, "dataClasses")= Named chr [1:3] "factor" "numeric" "factor"
## .. .. ..- attr(*, "names")= chr [1:3] "Survived" "Age" "Sex"
## $ coefnames : chr [1:2] "Age" "Sexmale"
## $ contrasts :List of 1
## $ xlevels :List of 1
## - attr(*, "class")= chr [1:2] "train" "train.formula"The model itself is always stored in the finalModel element. So to use the model in other functions, we would refer to it as age_sex_rf$finalModel.
Model statistics
age_sex_rf$finalModel##
## Call:
## randomForest(x = x, y = y, ntree = 200, mtry = param$mtry)
## Type of random forest: classification
## Number of trees: 200
## No. of variables tried at each split: 2
##
## OOB estimate of error rate: 24.3%
## Confusion matrix:
## Died Survived class.error
## Died 352 72 0.1698113
## Survived 101 187 0.3506944This tells us some important things:
- We used 200 trees
- At every potential branch, the model randomly used one of 2 variables to define the split
The out-of-bag (OOB) error rate
This requires further explanation. Because each tree is built from a bootstrapped sample, for any given tree approximately one-third of the observations are not used to build the tree. In essence, we have a natural validation set for each tree. For each observation, we predict the outcome of interest using all trees where the observation was not used to build the tree, then average across these predictions. For any observation, we should have \(K/3\) validation predictions where \(K\) is the total number of trees in the forest. Averaging across these predictions gives us an out-of-bag error rate for every observation (even if they are derived from different combinations of trees). Because the OOB estimate is built only using trees that were not fit to the observation, this is a valid estimate of the test error for the random forest.
Here we get an OOB estimate of the error rate of 24%. This means for test observations, the model misclassifies the individual’s survival 24% of the time.The confusion matrix - this compares the predictions to the actual known outcomes.
knitr::kable(age_sex_rf$finalModel$confusion)Died Survived class.error Died 352 72 0.1698113 Survived 101 187 0.3506944 The rows indicate the actual known outcomes, and the columns indicate the predictions. A perfect model would have 0s on the off-diagonal cells because every prediction is perfect. Clearly that is not the case. Not only is there substantial error, most it comes from misclassifying survivors. The error rate for those who actually died is much smaller than for those who actually survived.
Look at an individual tree
We could look at one tree generated by the model:
randomForest::getTree(age_sex_rf$finalModel, labelVar = TRUE)## left daughter right daughter split var split point status prediction
## 1 2 3 Sexmale 0.50 1 <NA>
## 2 4 5 Age 21.50 1 <NA>
## 3 6 7 Age 6.50 1 <NA>
## 4 8 9 Age 19.50 1 <NA>
## 5 10 11 Age 37.00 1 <NA>
## 6 12 13 Age 0.96 1 <NA>
## 7 14 15 Age 23.75 1 <NA>
## 8 16 17 Age 1.50 1 <NA>
## 9 18 19 Age 20.50 1 <NA>
## 10 20 21 Age 32.25 1 <NA>
## 11 22 23 Age 39.50 1 <NA>
## 12 0 0 <NA> 0.00 -1 Survived
## 13 24 25 Age 5.00 1 <NA>
## 14 26 27 Age 13.00 1 <NA>
## 15 28 29 Age 51.50 1 <NA>
## 16 0 0 <NA> 0.00 -1 Survived
## 17 30 31 Age 2.50 1 <NA>
## 18 0 0 <NA> 0.00 -1 Died
## 19 0 0 <NA> 0.00 -1 Died
## 20 32 33 Age 30.25 1 <NA>
## 21 0 0 <NA> 0.00 -1 Survived
## 22 0 0 <NA> 0.00 -1 Died
## 23 34 35 Age 56.50 1 <NA>
## 24 36 37 Age 3.50 1 <NA>
## 25 0 0 <NA> 0.00 -1 Survived
## 26 38 39 Age 10.00 1 <NA>
## 27 40 41 Age 22.50 1 <NA>
## 28 42 43 Age 44.50 1 <NA>
## 29 44 45 Age 77.00 1 <NA>
## 30 0 0 <NA> 0.00 -1 Died
## 31 46 47 Age 5.50 1 <NA>
## 32 48 49 Age 24.50 1 <NA>
## 33 50 51 Age 30.75 1 <NA>
## 34 52 53 Age 50.50 1 <NA>
## 35 54 55 Age 57.50 1 <NA>
## 36 56 57 Age 2.50 1 <NA>
## 37 0 0 <NA> 0.00 -1 Died
## 38 58 59 Age 8.50 1 <NA>
## 39 60 61 Age 11.50 1 <NA>
## 40 62 63 Age 16.50 1 <NA>
## 41 0 0 <NA> 0.00 -1 Died
## 42 64 65 Age 39.50 1 <NA>
## 43 66 67 Age 45.25 1 <NA>
## 44 68 69 Age 63.00 1 <NA>
## 45 0 0 <NA> 0.00 -1 Survived
## 46 70 71 Age 3.50 1 <NA>
## 47 72 73 Age 12.50 1 <NA>
## 48 74 75 Age 22.50 1 <NA>
## 49 76 77 Age 25.50 1 <NA>
## 50 0 0 <NA> 0.00 -1 Died
## 51 78 79 Age 31.50 1 <NA>
## 52 80 81 Age 43.50 1 <NA>
## 53 0 0 <NA> 0.00 -1 Survived
## 54 0 0 <NA> 0.00 -1 Died
## 55 0 0 <NA> 0.00 -1 Survived
## 56 82 83 Age 1.50 1 <NA>
## 57 0 0 <NA> 0.00 -1 Survived
## 58 84 85 Age 7.50 1 <NA>
## 59 0 0 <NA> 0.00 -1 Died
## 60 0 0 <NA> 0.00 -1 Survived
## 61 0 0 <NA> 0.00 -1 Survived
## 62 0 0 <NA> 0.00 -1 Died
## 63 86 87 Age 17.50 1 <NA>
## 64 88 89 Age 33.50 1 <NA>
## 65 90 91 Age 43.50 1 <NA>
## 66 0 0 <NA> 0.00 -1 Survived
## 67 92 93 Age 47.50 1 <NA>
## 68 94 95 Age 59.50 1 <NA>
## 69 0 0 <NA> 0.00 -1 Died
## 70 0 0 <NA> 0.00 -1 Survived
## 71 0 0 <NA> 0.00 -1 Survived
## 72 96 97 Age 7.50 1 <NA>
## 73 98 99 Age 14.25 1 <NA>
## 74 0 0 <NA> 0.00 -1 Survived
## 75 100 101 Age 23.50 1 <NA>
## 76 0 0 <NA> 0.00 -1 Died
## 77 102 103 Age 26.50 1 <NA>
## 78 0 0 <NA> 0.00 -1 Survived
## 79 0 0 <NA> 0.00 -1 Survived
## 80 104 105 Age 41.00 1 <NA>
## 81 106 107 Age 46.50 1 <NA>
## 82 0 0 <NA> 0.00 -1 Survived
## 83 0 0 <NA> 0.00 -1 Died
## 84 0 0 <NA> 0.00 -1 Died
## 85 0 0 <NA> 0.00 -1 Survived
## 86 0 0 <NA> 0.00 -1 Died
## 87 108 109 Age 18.50 1 <NA>
## 88 110 111 Age 32.50 1 <NA>
## 89 112 113 Age 35.50 1 <NA>
## 90 114 115 Age 40.25 1 <NA>
## 91 0 0 <NA> 0.00 -1 Died
## 92 0 0 <NA> 0.00 -1 Died
## 93 116 117 Age 49.50 1 <NA>
## 94 118 119 Age 53.00 1 <NA>
## 95 120 121 Age 60.50 1 <NA>
## 96 122 123 Age 6.50 1 <NA>
## 97 0 0 <NA> 0.00 -1 Died
## 98 0 0 <NA> 0.00 -1 Survived
## 99 124 125 Age 14.75 1 <NA>
## 100 0 0 <NA> 0.00 -1 Survived
## 101 0 0 <NA> 0.00 -1 Survived
## 102 0 0 <NA> 0.00 -1 Survived
## 103 126 127 Age 27.50 1 <NA>
## 104 0 0 <NA> 0.00 -1 Survived
## 105 0 0 <NA> 0.00 -1 Survived
## 106 128 129 Age 44.50 1 <NA>
## 107 130 131 Age 49.50 1 <NA>
## 108 0 0 <NA> 0.00 -1 Died
## 109 132 133 Age 19.50 1 <NA>
## 110 134 135 Age 31.50 1 <NA>
## 111 0 0 <NA> 0.00 -1 Died
## 112 136 137 Age 34.50 1 <NA>
## 113 138 139 Age 36.50 1 <NA>
## 114 0 0 <NA> 0.00 -1 Died
## 115 140 141 Age 41.50 1 <NA>
## 116 142 143 Age 48.50 1 <NA>
## 117 144 145 Age 50.50 1 <NA>
## 118 0 0 <NA> 0.00 -1 Died
## 119 0 0 <NA> 0.00 -1 Died
## 120 0 0 <NA> 0.00 -1 Died
## 121 146 147 Age 61.50 1 <NA>
## 122 0 0 <NA> 0.00 -1 Died
## 123 0 0 <NA> 0.00 -1 Survived
## 124 0 0 <NA> 0.00 -1 Died
## 125 148 149 Age 15.50 1 <NA>
## 126 0 0 <NA> 0.00 -1 Survived
## 127 150 151 Age 29.50 1 <NA>
## 128 0 0 <NA> 0.00 -1 Survived
## 129 0 0 <NA> 0.00 -1 Survived
## 130 152 153 Age 48.50 1 <NA>
## 131 0 0 <NA> 0.00 -1 Survived
## 132 0 0 <NA> 0.00 -1 Died
## 133 154 155 Age 20.75 1 <NA>
## 134 156 157 Age 29.50 1 <NA>
## 135 0 0 <NA> 0.00 -1 Died
## 136 0 0 <NA> 0.00 -1 Died
## 137 0 0 <NA> 0.00 -1 Died
## 138 0 0 <NA> 0.00 -1 Died
## 139 158 159 Age 37.50 1 <NA>
## 140 0 0 <NA> 0.00 -1 Died
## 141 160 161 Age 42.50 1 <NA>
## 142 0 0 <NA> 0.00 -1 Died
## 143 0 0 <NA> 0.00 -1 Survived
## 144 0 0 <NA> 0.00 -1 Died
## 145 0 0 <NA> 0.00 -1 Died
## 146 0 0 <NA> 0.00 -1 Died
## 147 0 0 <NA> 0.00 -1 Died
## 148 0 0 <NA> 0.00 -1 Survived
## 149 162 163 Age 18.50 1 <NA>
## 150 164 165 Age 28.50 1 <NA>
## 151 0 0 <NA> 0.00 -1 Survived
## 152 0 0 <NA> 0.00 -1 Survived
## 153 0 0 <NA> 0.00 -1 Survived
## 154 166 167 Age 20.25 1 <NA>
## 155 168 169 Age 21.50 1 <NA>
## 156 170 171 Age 26.50 1 <NA>
## 157 172 173 Age 30.75 1 <NA>
## 158 0 0 <NA> 0.00 -1 Survived
## 159 174 175 Age 38.50 1 <NA>
## 160 0 0 <NA> 0.00 -1 Died
## 161 0 0 <NA> 0.00 -1 Died
## 162 176 177 Age 17.50 1 <NA>
## 163 0 0 <NA> 0.00 -1 Survived
## 164 0 0 <NA> 0.00 -1 Survived
## 165 0 0 <NA> 0.00 -1 Survived
## 166 0 0 <NA> 0.00 -1 Died
## [ reached getOption("max.print") -- omitted 25 rows ]Unfortunately there is no easy plotting mechanism for the result of getTree.7
Yikes. Clearly this tree is pretty complicated. Not something we want to examine directly.
Variable importance
Another method of interpreting random forests looks at the importance of individual variables in the model.
varImpPlot(age_sex_rf$finalModel)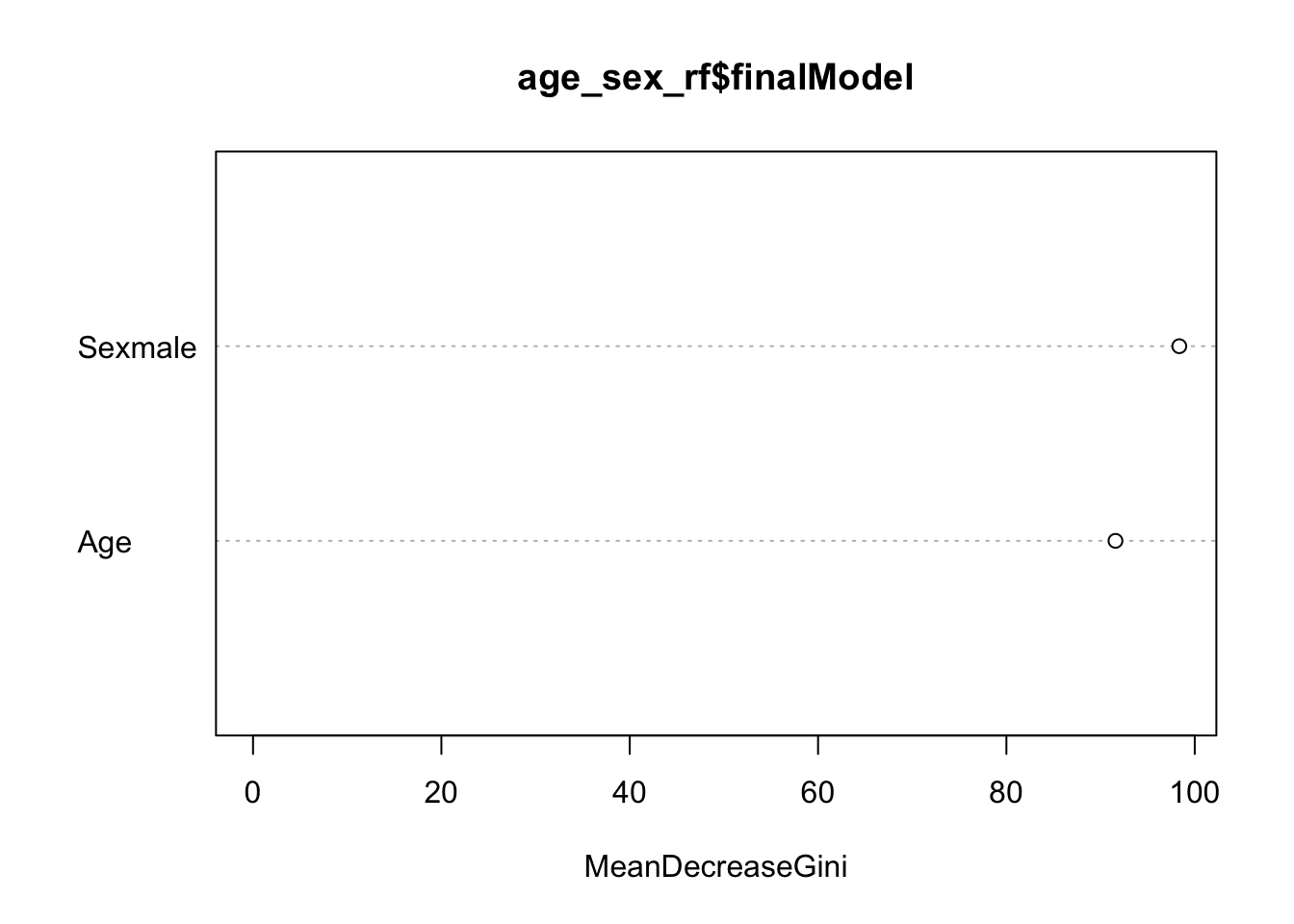
This tells us how much each variable decreases the average Gini index, a measure of how important the variable is to the model. Essentially, it estimates the impact a variable has on the model by comparing prediction accuracy rates for models with and without the variable. Larger values indicate higher importance of the variable. Here we see that the gender variable Sexmale is most important.
Prediction
We can also use random forests to make predictions on an explicit validation set, rather than relying on OOB estimates. Let’s split our Titanic data into training and test sets, train the full random forest model on the training set, then use that model to predict outcomes in the test set. Instead of using a bootstrapped resampling method, again let’s use "oob":
titanic_split <- resample_partition(titanic_rf_data,
c(test = 0.3, train = 0.7))
titanic_train <- titanic_split$train %>%
tbl_df()
titanic_test <- titanic_split$test %>%
tbl_df()
rf_full <- train(Survived ~ Pclass + Sex + Age + SibSp +
Parch + Fare + Embarked,
data = titanic_train,
method = "rf",
ntree = 500,
trControl = trainControl(method = "oob"))
rf_full$finalModel##
## Call:
## randomForest(x = x, y = y, ntree = 500, mtry = param$mtry)
## Type of random forest: classification
## Number of trees: 500
## No. of variables tried at each split: 2
##
## OOB estimate of error rate: 19.04%
## Confusion matrix:
## Died Survived class.error
## Died 270 28 0.09395973
## Survived 67 134 0.33333333- We used 500 trees
- At every potential branch, the model randomly used one of 2 variables to define the split
- For OOB test observations, the model misclassifies the individual’s survival 19% of the time.
- This model is somewhat better at predicting survivors compared to the age + gender model, but is still worse at predicting survivors from the deceased. This is not terribly surprising since our classes are unbalanced. That is, there were a lot fewer survivors (342) than deceased (549). Because of this, the model has more information on those that died than those that lived, so it is natural to have better predictions for those that died.
varImpPlot(rf_full$finalModel)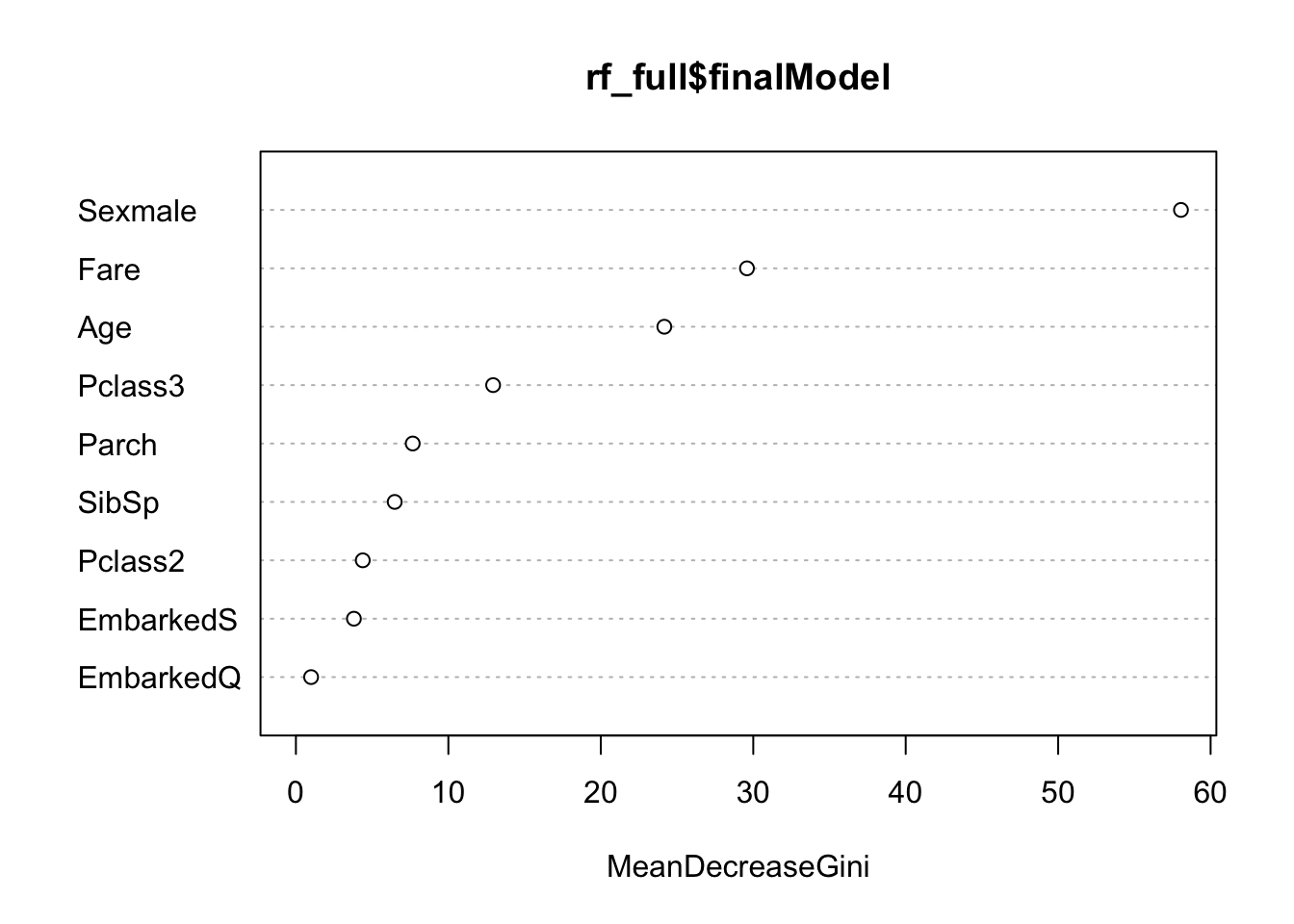
Note that gender and age are important predictors in the random forest, but so too is the fare an individual paided. This is a proxy for socioeconomic status; recall that the wealthy had better access to lifeboats.
To make predictions for the validation set, we use the predict function. By setting type = "prob" we will get predicted probabilities for each possible outcome, rather than just a raw prediction of “Survived” or “Died”:
titanic_pred <- titanic_test %>%
bind_cols(predict(rf_full, newdata = titanic_test, type = "prob") %>%
rename(prob_dead = Died,
prob_survive = Survived))
titanic_pred## # A tibble: 213 × 10
## Survived Pclass Sex Age SibSp Parch Fare Embarked prob_dead
## <fctr> <fctr> <fctr> <dbl> <int> <int> <dbl> <fctr> <dbl>
## 1 Survived 3 female 26 0 0 7.9250 S 0.536
## 2 Died 3 male 35 0 0 8.0500 S 0.996
## 3 Survived 2 female 14 1 0 30.0708 C 0.110
## 4 Died 3 male 20 0 0 8.0500 S 0.998
## 5 Died 2 male 35 0 0 26.0000 S 0.940
## 6 Survived 2 male 34 0 0 13.0000 S 0.972
## 7 Survived 3 female 38 1 5 31.3875 S 0.910
## 8 Died 1 male 19 3 2 263.0000 S 0.584
## 9 Died 1 male 40 0 0 27.7208 C 0.734
## 10 Died 2 male 66 0 0 10.5000 S 0.864
## # ... with 203 more rows, and 1 more variables: prob_survive <dbl>Acknowledgments
- For more information on statistical learning and the math behind these methods, see the awesome book An Introduction to Statistical Learning
Session Info
devtools::session_info()## setting value
## version R version 3.3.1 (2016-06-21)
## system x86_64, darwin13.4.0
## ui RStudio (1.0.44)
## language (EN)
## collate en_US.UTF-8
## tz America/Chicago
## date 2016-11-16
##
## package * version date source
## assertthat 0.1 2013-12-06 CRAN (R 3.3.0)
## boot * 1.3-18 2016-02-23 CRAN (R 3.3.1)
## broom * 0.4.1 2016-06-24 CRAN (R 3.3.0)
## car 2.1-3 2016-08-11 CRAN (R 3.3.0)
## caret * 6.0-73 2016-11-10 CRAN (R 3.3.2)
## class 7.3-14 2015-08-30 CRAN (R 3.3.1)
## codetools 0.2-15 2016-10-05 CRAN (R 3.3.0)
## colorspace 1.2-7 2016-10-11 CRAN (R 3.3.0)
## DBI 0.5-1 2016-09-10 CRAN (R 3.3.0)
## devtools 1.12.0 2016-06-24 CRAN (R 3.3.0)
## digest 0.6.10 2016-08-02 CRAN (R 3.3.0)
## dplyr * 0.5.0 2016-06-24 CRAN (R 3.3.0)
## e1071 1.6-7 2015-08-05 CRAN (R 3.3.0)
## evaluate 0.10 2016-10-11 CRAN (R 3.3.0)
## foreach 1.4.3 2015-10-13 CRAN (R 3.3.0)
## foreign 0.8-67 2016-09-13 CRAN (R 3.3.0)
## formatR 1.4 2016-05-09 CRAN (R 3.3.0)
## gapminder * 0.2.0 2015-12-31 CRAN (R 3.3.0)
## gganimate * 0.1 2016-11-11 Github (dgrtwo/gganimate@26ec501)
## ggplot2 * 2.2.0 2016-11-10 Github (hadley/ggplot2@f442f32)
## gtable 0.2.0 2016-02-26 CRAN (R 3.3.0)
## highr 0.6 2016-05-09 CRAN (R 3.3.0)
## htmltools 0.3.5 2016-03-21 CRAN (R 3.3.0)
## htmlwidgets 0.8 2016-11-09 CRAN (R 3.3.1)
## ISLR * 1.0 2013-06-11 CRAN (R 3.3.0)
## iterators 1.0.8 2015-10-13 CRAN (R 3.3.0)
## jsonlite 1.1 2016-09-14 CRAN (R 3.3.0)
## knitr 1.15 2016-11-09 CRAN (R 3.3.1)
## labeling 0.3 2014-08-23 CRAN (R 3.3.0)
## lattice * 0.20-34 2016-09-06 CRAN (R 3.3.0)
## lazyeval 0.2.0 2016-06-12 CRAN (R 3.3.0)
## lme4 1.1-12 2016-04-16 cran (@1.1-12)
## lubridate * 1.6.0 2016-09-13 CRAN (R 3.3.0)
## magrittr 1.5 2014-11-22 CRAN (R 3.3.0)
## MASS 7.3-45 2016-04-21 CRAN (R 3.3.1)
## Matrix 1.2-7.1 2016-09-01 CRAN (R 3.3.0)
## MatrixModels 0.4-1 2015-08-22 CRAN (R 3.3.0)
## memoise 1.0.0 2016-01-29 CRAN (R 3.3.0)
## mgcv 1.8-16 2016-11-07 CRAN (R 3.3.0)
## minqa 1.2.4 2014-10-09 cran (@1.2.4)
## mnormt 1.5-5 2016-10-15 CRAN (R 3.3.0)
## ModelMetrics 1.1.0 2016-08-26 CRAN (R 3.3.0)
## modelr * 0.1.0 2016-08-31 CRAN (R 3.3.0)
## munsell 0.4.3 2016-02-13 CRAN (R 3.3.0)
## nlme 3.1-128 2016-05-10 CRAN (R 3.3.1)
## nloptr 1.0.4 2014-08-04 cran (@1.0.4)
## nnet 7.3-12 2016-02-02 CRAN (R 3.3.1)
## pbkrtest 0.4-6 2016-01-27 CRAN (R 3.3.0)
## plyr 1.8.4 2016-06-08 CRAN (R 3.3.0)
## profvis * 0.3.2 2016-05-19 CRAN (R 3.3.0)
## psych 1.6.9 2016-09-17 cran (@1.6.9)
## purrr * 0.2.2 2016-06-18 CRAN (R 3.3.0)
## quantreg 5.29 2016-09-04 CRAN (R 3.3.0)
## R6 2.2.0 2016-10-05 CRAN (R 3.3.0)
## randomForest * 4.6-12 2015-10-07 CRAN (R 3.3.0)
## rcfss * 0.1.0 2016-10-06 local
## Rcpp 0.12.7 2016-09-05 cran (@0.12.7)
## readr * 1.0.0 2016-08-03 CRAN (R 3.3.0)
## readxl * 0.1.1 2016-03-28 CRAN (R 3.3.0)
## reshape2 1.4.2 2016-10-22 CRAN (R 3.3.0)
## rmarkdown * 1.1 2016-10-16 CRAN (R 3.3.1)
## rsconnect 0.5 2016-10-17 CRAN (R 3.3.0)
## rstudioapi 0.6 2016-06-27 CRAN (R 3.3.0)
## scales 0.4.1 2016-11-09 CRAN (R 3.3.1)
## SparseM 1.72 2016-09-06 CRAN (R 3.3.0)
## stringi 1.1.2 2016-10-01 CRAN (R 3.3.0)
## stringr * 1.1.0 2016-08-19 cran (@1.1.0)
## tibble * 1.2 2016-08-26 cran (@1.2)
## tidyr * 0.6.0 2016-08-12 CRAN (R 3.3.0)
## tidyverse * 1.0.0 2016-09-09 CRAN (R 3.3.0)
## tree * 1.0-37 2016-01-21 CRAN (R 3.3.0)
## withr 1.0.2 2016-06-20 CRAN (R 3.3.0)
## yaml 2.1.13 2014-06-12 CRAN (R 3.3.0)The actual value you use is irrelevant. Just be sure to set it in the script, otherwise R will randomly pick one each time you start a new session.↩
Because
modelris a work in progress, it doesn’t always play nicely with base R functions. Note how I refer directly to the test↩pretty = 0cleans up the formatting of the text some.↩Specifically passenger class, gender, age, number of sibling/spouses aboard, number of parents/children aboard, fare, and port of embarkation.↩
Because behind the scenes,
caretis simply using theglmfunction to train the model.↩There are many packages that use algorithms to estimate random forests. They all do the same basic thing, though with some notable differences. The
rfmethod is generally popular, so I use it here.↩Remember that it was not generated by the
treelibrary, but instead by a function inrandomForest. Because of that we cannot just callplot(age_sex_rf$finalModel).↩
This work is licensed under the CC BY-NC 4.0 Creative Commons License.
